BERTRAND RUSSELL & ALFRED NORTH WHITEHEAD – Principia Mathematica 1+1=2
 |
Bertrand Russell (1872-1970) and A.N. Whitehead (1861-1947) |
Bertrand Russell and Alfred North Whitehead were British mathematicians, logicians and philosophers, who were in the vanguard of the British revolt against Continental idealism in the early 20th Century and, between them, they made important contributions in the fields of mathematical logic and set theory.
Whitehead was the elder of the two and came from a more pure mathematics background. He became Russell’s tutor at Trinity College, Cambridge in the 1890s, and then collaborated with his more celebrated ex-student in the first decade of the 20th Century on their monumental work, the “Principia Mathematica”. After the First World War, though, much of which Russell spent in prison due to his pacifist activities, the collaboration petered out, and Whitehead’s academic career remained ever after in the shadow of that of the more flamboyant Russell. He emigrated to the United States in the 1920s, and spent the rest of his life there.
Russell was born into a wealthy family of the British aristocracy, although his parents were extremely liberal and radical for the times. His parents died when Russell was quite young and he was largely brought up by his staunchly Victorian (although quite progressive) grandmother. His adolescence was very lonely and he suffered from bouts of depression, later claiming that it was only his love of mathematics that kept him from suicide. He studied mathematics and philosophy at Cambridge University under G.E. Moore and A.N. Whitehead, where he developed into an innovative philosopher, a prolific writer on many subjects, a committed atheist and an inspired mathematician and logician. Today, he is considered one of the founders of analytic philosophy, but he wrote on almost every major area of philosophy, particularly metaphysics, ethics, epistemology, the philosophy of mathematics and the philosophy of language.
Russell was a committed and high-profile political activist throughout his long life. He was a prominent anti-war activist during both the First and Second World Wars, championed free trade and anti-imperialism, and later became a strident campaiger for nuclear disarmament and socialism, and against Adolf Hitler, Soviet totalitarianism and the USA’s involvement in the Vietnam War.
Russell’s Paradox
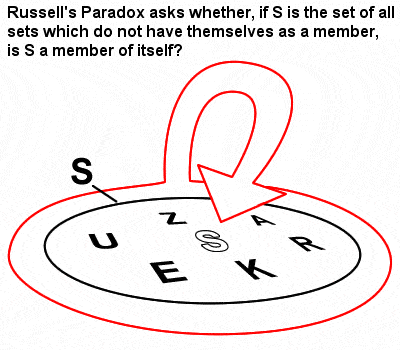 |
Russell’s Paradox |
Russell’s mathematics was greatly influenced by the set theory and logicism Gottlob Frege had developed in the wake of Cantor‘s groundbreaking early work on sets. In his 1903 “The Principles of Mathematics”, though, he identified what has come to be known as Russell’s Paradox (a set containing sets that are not members of themselves), which showed that Frege’s naive set theory could in fact lead to contradictions.
The paradox is sometimes illustrated by this simplistic example: “If a barber shaves all and only those men in the village who do not shave themselves, does he shave himself?“
The paradox seemed to imply that the very foundations of the whole of mathematics could no longer be trusted, and that, even in mathematics, the truth could never be known absolutely (Gödel‘s and Turing‘s later work would only make this worse). Russell’s criticism was enough to rock Frege’s confidence in the entire edifice of logicism, and he was gracious enough to admit this openly in a hastily written appendix to Volume II of his “Basic Laws of Arithmetic”.
But Russell’s magnum opus was the monolithic “Principia Mathematica”, published in three volumes in 1910, 1912 and 1913. The first volume was co-written by Whitehead, although the later two were almost all Russell’s work. The aspiration of this ambitious work was nothing less than an attempt to derive all of mathematics from purely logical axioms, while avoiding the kinds of paradoxes and contradictions found in Frege’s earlier work on set theory. Russell achieved this by employing a theory or system of “types”, whereby each mathematical entity is assigned to a type within a hierarchy of types, so that objects of a given type are built exclusively from objects of preceding types lower in the hierarchy, thus preventing loops. Each set of elements, then, is of a different type than each of its elements, so that one can not speak of the “set of all sets” and similar constructs, which lead to paradoxes.
However, the “Principia” required, in addition to the basic axioms of type theory, three further axioms that seemed to not be true as mere matters of logic, namely the “axiom of infinity” (which guarantees the existence of at least one infinite set, namely the set of all natural numbers), the “axiom of choice” (which ensures that, given any collection of “bins”, each containing at least one object, it is possible to make a selection of exactly one object from each bin, even if there are infinitely many bins, and that there is no “rule” for which object to pick from each) and Russell’s own “axiom of reducibility” (which states that any propositional truth function can be expressed by a formally equivalent predicative truth function).
During the ten years or so that Russell and Whitehead spent on the “Principia”, draft after draft was begun and abandoned as Russell constantly re-thought his basic premises. Russell and his wife Alys even moved in with the Whiteheads in order to expedite the work, although his own marriage suffered as Russell became infatuated with Whitehead’s young wife, Evelyn. Eventually, Whitehead insisted on publication of the work, even if it was not (and might never be) complete, although they were forced to publish it at their own expense as no commercial publishers would touch it.
Principia Mathematica
 |
A small part of the long proof that 1+1 =2 in the “Principia Mathematica” |
Some idea of the scope and comprehensiveness of the “Principia” can be gleaned from the fact that it takes over 360 pages to prove definitively that 1 + 1 = 2.
Today, it is widely considered to be one of the most important and seminal works in logic since Aristotle’s “Organon”. It seemed remarkably successful and resilient in its ambitious aims, and soon gained world fame for Russell and Whitehead. Indeed, it was only Gödel’s 1931 incompleteness theorem that finally showed that the “Principia” could not be both consistent and complete.
Russell was awarded the Order of Merit in 1949 and the Nobel Prize in Literature in the following year. His fame continued to grow, even outside of academic circles, and he became something of a household name in later life, although largely as a result of his philosophical contributions and his political and social activism, which he continued until the end of his long life. He died of influenza in his beloved Wales at the grand old age of 97.
<< Back to Hardy and Ramanujan | Forward to Hilbert >> |
