JUMP TO TOPIC
4 Times Table – Explanation & Examples
The 4 times table is quite similar to the 2 times table. Just like the multiples of 2, all the multiples of the digit 4 are also even numbers, and so it is easy to understand and memorize.
The 4 times table is a table that contains multiples of the number 4.
Learning and understanding the 4 times table is essential for solving mathematical problems related to multiplication, division, and factorization. This topic will provide interesting tips and tricks to learning and the 4 times table quickly.
You should refresh the following concepts to understand this topic easily.
- Basics of addition and multiplication
- 1 times Table
- 2 times table
- 3 times table
4 Multiplication Table
We can write the table of 4 as follows:
- $4 \times1 = 4$
- $4 \times 2 = 8$
- $4 \times 3 = 12$
- $4 \times 4 =16$
- $4 \times 5 =20$
- $4 \times 6 =24$
- $4 \times 7 = 28$
- $4 \times 8 = 32$
- $4 \times 9 = 36$
- $4 \times 10 = 40$
Different Tips To Learn the 4 Times Table Quickly
Let us look at some simple tips which can help you memorize the 4 times table.
Using the 2 times table: One of the easiest ways to learn the 4 times table is using the 2 times table. This method involves adding the outcomes of the 2 times table with themselves, as shown in the table below.
2 Times Table | Addition | (Answer) | 4 Times Table |
$2 \times 1 = 2$ | $2 + 2$ | $4$ | $ 4 \times 1 = 4$ |
$2 \times 2 = 4$ | $4 + 4$ | $8$ | $4 \times 2 = 8$ |
$2 \times 3 = 6$ | $6 + 6$ | $12$ | $4 \times 3 = 12$ |
$2 \times 4 = 8$ | $8 + 8$ | $16$ | $4 \times 4 =16$ |
$2 \times 5 = 10$ | $10 + 10$ | $20$ | $4 \times 5 =20$ |
$2 \times 6 = 12$ | $12 + 12$ | $24$ | $4 \times 6 =24$ |
$2 \times 7 = 14$ | $14 + 14$ | $28$ | $4 \times 7 = 28$ |
$2 \times 8 = 16$ | $16 + 16$ | $32$ | $4 \times 8 = 32$ |
$2 \times 9 = 18$ | $18 + 18$ | $36$ | $4 \times 9 = 36$ |
$2 \times 10 = 20$ | $20 + 20$ | $40$ | $4 \times 10 = 40$ |
As we can see in the first row, the answer of $2\times 1$ is $2$, and if we add the answer to itself, i.e. $2+2$, we get $4$, which is also equal to $4\times 1 = 4$. Similarly, in the fifth row, we have $2\times 5 = 10$ and if we add $10$ to itself we get $10+10 =20$ which is equal to $4 \times 5$.
Using the 3 times table: If you have already learned the three times table, then this method is the best as it will help you revise the 3 times table and learn the 4 times table simultaneously.
3 Times Table | Addition | (Answer) |
$3\times 1 = 3$ | $3 + 1$ | $4$ |
$3\times 2 = 6$ | $6 + 2$ | $8$ |
| $3\times 3 = 9$ | $9 + 3$ | $12$ |
$3\times 4 = 12$ | $12 + 4$ | $16$ |
| $3\times 5 = 15$ | $15 + 5$ | $20$ |
$3\times 6 = 18$ | $18 + 6$ | $24$ |
$3 \times 7 = 21$ | $21 + 7$ | $28$ |
| $3 \times 8 = 24$ | $24 + 8$ | $32$ |
$3 \times 9 = 27$ | $27 + 9$ | $36$ |
| $3 \times 10 = 30$ | $30 + 10$ | $40$ |
In this method, we add the natural numbers, 1, 2, 3, and so on to the outcomes of the 3 times table. For example, the first multiple of the 3 times table, i.e., $3\times 1 = 3$ will be added with the first natural number, $1$ and the second multiple of the 3 times table $3\times 2 = 6$ will be added with the second natural number, $2$ and so on. The results will give us the 4 times table.
Recitation: Students who are having difficulty in addition or the multiplication method can recite the 4 times loudly and repeatedly. Once they have memorized it, it will be easier for them to develop a basic understanding. You can read this out loud.
1 times 4 is 4
2 times 4 is 8
3 times 4 is 12
4 Times 4 is 16
5 times 4 is 20
6 times 4 is 24
7 times 4 is 28
8 times 4 is 32
9 times 4 is 36
10 times 4 is 40
Table of 4 From 1 to 20:
We can write a complete table of 4 from 1 to 20 as follows:
Numerical Representation | Descriptive Representation | Product (Answer) |
$4 \times 1$ | Four times one | $4$ |
| $4 \times 2$ | Four times two | $8$ |
$4 \times 3$ | Four times three | $12$ |
$4 \times 4$ | Four times four | $16$ |
| $4 \times 5$ | Four times five | $20$ |
$4 \times 6$ | Four times six | $24$ |
| $4 \times 7$ | Four times seven | $28$ |
$4 \times 8$ | Four times eight | $32$ |
| $4 \times 9$ | Four times nine | $36$ |
$4 \times 10$ | Four times ten | $40$ |
| $4 \times 11$ | Four times eleven | $44$ |
$4 \times 12$ | Four times twelve | $48$ |
| $4 \times 13$ | Four times thirteen | $52$ |
$4 \times 14$ | Four times fourteen | $56$ |
| $4 \times 15$ | Four times fifteen | $60$ |
$4 \times 16$ | Four times sixteen | $64$ |
$4 \times 17$ | Four times seventeen | $68$ |
$4 \times 18$ | Four times eighteen | $72$ |
| $4 \times 19$ | Four times nineteen | $76$ |
$4 \times 20$ | Four times twenty | $80$ |
This table also shows an interesting pattern. After the 10th multiple of 4, which is $4\times 10 = 40$, the last digit of the answers of the next 10 multiples will be equal to the last digit of the first 10 multiples. For example, $4\times 1= 4$ and $4\times 11 =44$; the last digit of the 11th multiple is the same as the first multiple of 4. Similarly, $4\times 3= 12$ and $4\times 13= 52$, so the last digits of the 3rd and the 13th multiples of 4 are the same. The green digits show this pattern in the figure below.
Example 1: Alex has six plastic bags. His father has given him two dozen oranges and asked him to put the oranges in the bags with the condition that all the bags should contain an equal number of oranges.
Solution:
Alex knows $1$ dozen = $12$.
So $2$ dozen oranges will be: $12+12 = 24$.
Alex has recently learned the 4 times table and knows that $4\times 6 =24$.
So if Alex puts $4$ oranges in each bag, he will have the same number of oranges in 6 bags.
Example 2: Using the 4 times table, calculate $4$ times $6$ plus $10$?
Solution:
$4$ times $6$ plus $10$ can be written as $4\times 6 +10$. Using the DMAS rule (Division, Multiplication, Addition, and Subtraction), we will first multiply $4$ and $6$ and then add $10$.
$(4\times6) + 10$
$24+10 = 34$
Example 3: Steve spends $4$ dollars each week. Calculate how much Steve would spend in four weeks? And how much would he spend in seven weeks?
Solution:
The amount spent by Steve in four weeks can be calculated as $4\times 4 =16$ dollars. Similarly, the amount spent in seven weeks would be $4 \times 7 = 28$ dollars.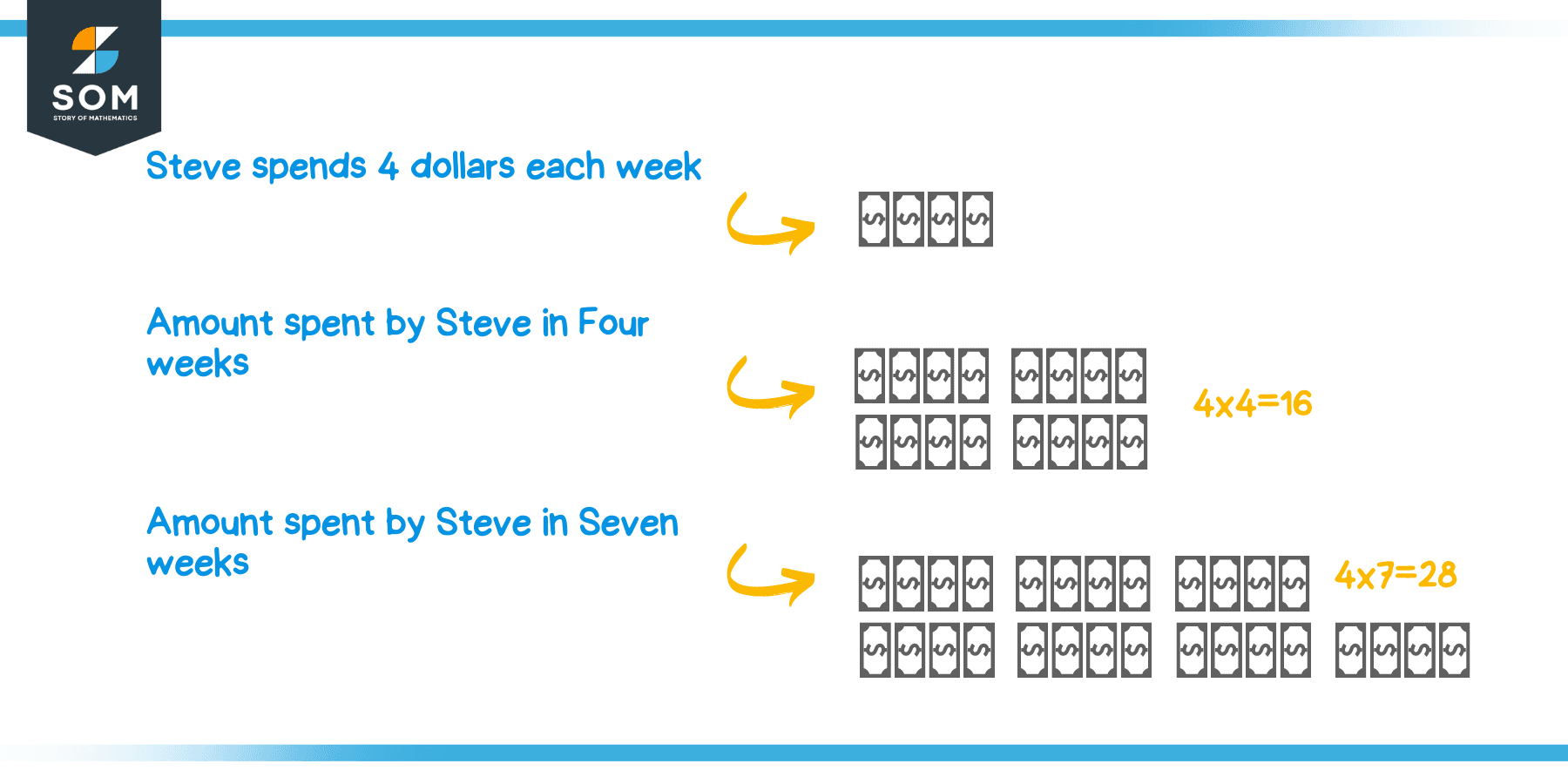
Practice Questions:
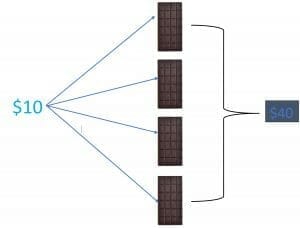
- Harris wants to purchase four chocolates, and the price of one chocolate is $10$ dollars. Calculate the total cost of four chocolates using the 4 times table.
- What is the answer of 4 times 4 minus 10?
- What is the 8th multiple of 4?
- From the given table, select the numbers which are multiples of 4.
| 22 | 21 | 36 | 40 | 5 |
| 25 | 19 | 20 | 12 | 10 |
| 9 | 1 | 3 | 17 | 15 |
| 10 | 18 | 14 | 16 | 20 |
| 31 | 2 | 10 | 25 | 21 |
| 32 | 14 | 15 | 29 | 30 |
| 46 | 32 | 31 | 34 | 35 |
| 37 | 37 | 26 | 39 | 40 |
| 41 | 42 | 43 | 51 | 45 |
| 44 | 48 | 59 | 49 | 60 |
5. A car covers four kilometers in a lap. Calculate total distance covered by the car if
a) It has completed 10 laps
b) It has completed 8 laps
c) It has completed 20 laps
Answer Key
1) The cost of One chocolate is $10$ dollars.
Then by using 4 times table, the cost of four chocolates will be:
$4\times 10 = 40$ dollars
2) $4$ times $4$ minus $10$ can be written as $4 \times4-10$. By using the DMAS rule $(4\times4)-10= 16-10 = 4 $
3) The 8th multiple of 4 is $4 \times 8 = 32$
4)
| 22 | 21 | 36 | 40 | 5 |
| 25 | 19 | 20 | 12 | 10 |
| 9 | 1 | 3 | 17 | 15 |
| 10 | 18 | 14 | 16 | 28 |
| 31 | 2 | 10 | 25 | 21 |
| 32 | 14 | 15 | 29 | 30 |
| 46 | 32 | 31 | 34 | 35 |
| 37 | 37 | 26 | 39 | 40 |
| 41 | 42 | 43 | 51 | 45 |
| 44 | 48 | 59 | 49 | 60 |
5) Car covers 4 KMs in one lap
a) If the car completes 10 laps. The total distance covered can be calculated using 4 times table as:
$4 \times 10 = 40$ KM
b) If the car completes 8 laps then the total distance covered is $4 \times 8 = 32$ KM
c) If the car completes 20 laps, then the total distance covered is $4 \times 20 = 80$ KM