JUMP TO TOPIC
9 times table – Explanation & Examples
 The 9 times table is one of the most important tables in mathematics as 9 is an odd number, and it is also a perfect square. So, students must learn and memorize this table to solve complex math problems.
The 9 times table is one of the most important tables in mathematics as 9 is an odd number, and it is also a perfect square. So, students must learn and memorize this table to solve complex math problems.
The 9 times table is a table that has multiples of the number 9.
Learning and understanding the 9 times table is essential for solving multiplication, division, and factorization-related mathematical problems. The 9 times table follows some easy-to-learn patterns that can help in learning this table.
We will discuss these patterns and some other tips to help you memorize this table. You should refresh the following concepts to understand this topic easily.
- Basics of addition and multiplication.
- Three times table
- Six times table
- Eight times table
9 multiplication table
The table of 9 can be written as:
- $9\times1 = 9$
- $9 \times 2 = 18$
- $9 \times 3 = 27$
- $9 \times 4 =36$
- $9 \times 5 =45$
- $9 \times 6 =54$
- $9 \times 7 = 63$
- $9 \times 8 = 72$
- $9 \times 9 = 81$
- $9 \times 10 = 90$
Different tips for the 9 times table:
Let us discuss some of the tips and tricks that will help students quickly learn and memorize this table.
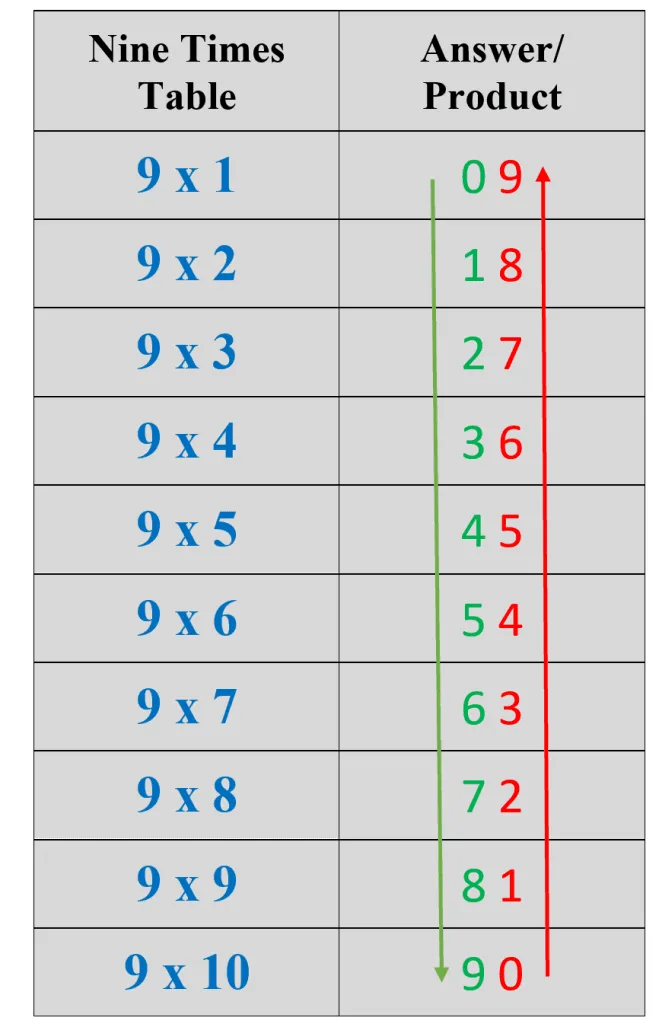
Digits Pattern: The digit pattern for the 9 times table is easy to learn and understand. The unit digit of the outcomes of the 9 times table increases from 0 to 9, while and the tens digit of the outcomes decreases from 9 to 0, as shown in the picture below.
Fingers Method: This method is quite easy and simple. All you have to do is put forward both of your hands and open your fingers. Let say we want to calculate 9 times 4. Counting from the left-hand thumb, close the fourth finger. Now count the fingers starting from the left-hand thumb till you reach the closed finger. In this example, we will count three fingers till we reach the fourth finger, which is closed.
This gives us the tens digit of the product 9 times 4. Now starting from the closed finger, count the remaining fingers to the right of the closed finger. We can count 6 fingers to the right of the closed finger, as shown in the figure below. This gives the unit digit of the product 9 times 4. So the unit digit is 6, and the tens digit is 3, and if we combine them, we get 36 which is equal to 9 times 4.
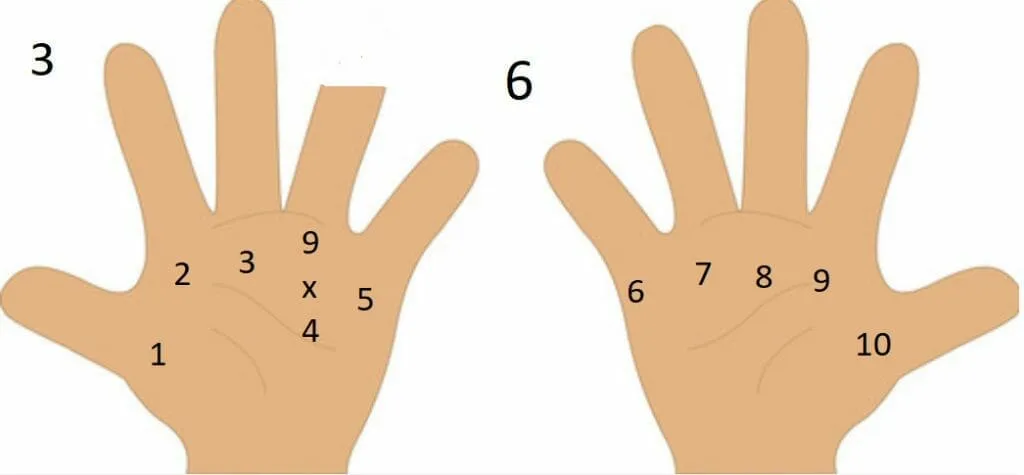
Similarly, if we want to calculate 9 times 3, close the third figure starting from the left-hand thumb. We have 2 fingers on the left side of the closed finger and 7 on the right side. Combining them, we get 27 which is equal to 9 times 3.
Using the 8 times table: This method is also easy and effective. This method also helps in the revision of the 8 times table. In this method, we add natural numbers to the multiples of the number 8 to get the 9 times table.
The first multiple of 8 is added with the first natural number, i.e., 1. The second multiple of number 8 is added with the second natural number, i.e., 2 and so on. This method is presented in the table below.
Eight Times Table | Addition | (Addition Outcome) | Nine Times Table |
8 x 1 = 8 | 8 + 1 | 9 | 9 x 1 = 9 |
8 x 2 = 16 | 16 + 2 | 18 | 9 x 2 = 18 |
8 x 3 = 24 | 24 + 3 | 27 | 9 x 3 = 27 |
8 x 4 = 32 | 32 + 4 | 36 | 9 x 4 =36 |
8 x 5 = 40 | 40 + 5 | 45 | 9 x 5 =45 |
8 x 6 = 48 | 48 + 6 | 54 | 9 x 6 =54 |
8 x 7 = 56 | 56 + 7 | 63 | 9 x 7 = 63 |
8 x 8 = 64 | 64 + 8 | 72 | 9 x 8 = 72 |
8 x 9 = 72 | 72 + 9 | 81 | 9 x 9 = 81 |
8 x 10 = 80 | 80 + 10 | 90 | 9 x 10 = 90 |
Using the 6 and the 3 times table: This method is simple, and it will help students in the revision of the 3 and the 6 times table. The only downside is that it is time-consuming. In this method, we write both the 6 and 3 times tables and then add their outcomes.
For example, the sixth multiple of 6 is 36; while, the sixth multiple of 3 is 18. If we add them up, we get $36+18 =54$, which is the sixth multiple of 9. So by adding the corresponding multiples of 3 and 6, we can form the nine times table, as shown below.
Six Times Table | Three Times Table | (Addition) | (Addition Outcome) |
6 x 1 = 6 | 3 x 1 = 3 | 6 + 3 | 9 x 1 = 9 |
6 x 2 = 12 | 3 x 2 = 6 | 12 + 6 | 9 x 2 = 18 |
6 x 3 = 18 | 3 x 3 = 9 | 18 + 9 | 9 x 3 = 27 |
6 x 4 = 24 | 3 x 4 = 12 | 24 + 12 | 9 x 4 =36 |
6 x 5 = 30 | 3 x 5 = 15 | 30 + 15 | 9 x 5 =45 |
6 x 6 = 36 | 3 x 6 = 18 | 36 + 18 | 9 x 6 =54 |
6 x 7 = 42 | 3 x 7 = 21 | 42 + 21 | 9 x 7 = 63 |
6 x 8 = 48 | 3 x 8 = 24 | 48 + 24 | 9 x 8 = 72 |
6 x 9 = 54 | 3 x 9 = 27 | 54 + 27 | 9 x 9 = 81 |
6 x 10 = 60 | 3 x 10 = 30 | 60 + 30 | 9 x 10 = 90 |
Addition: This is a universal method that can be applied to any table. It is an easy and effective method but requires some time and patience. This method is useful if students are having trouble learning previous tips and tricks.
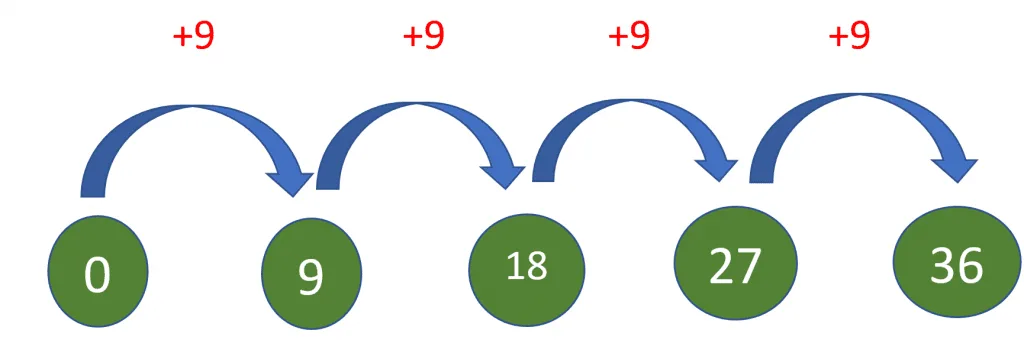
Students can use this method and the recitation of 9 times table to help them memorize the table quickly. In this method, we add 9 to 0, and the answer is again added with 9, which continues as shown in the picture below.
Recitation: This method is for those students who have difficulty understanding the previous tips, such as basic addition and multiplication. Students can recite the 8 times loudly and repeatedly to help them memorize the table, and then they can focus on learning the other tips and skills.
Recitation can be done like:
- Nine times one is 9
- Nine times two is 18
- Nine times three is 27
- Nine times four is 36
- Nine times five is 45
- Nine times six is 54
- Nine times seven is 63
- Nine times eight is 72
- Nine times nine is 81
- Nine times ten is 90
Table of 9 from 1 to 20:
A complete table of 9 from 1 to 20 can be written as:
Numerical Representation | Descriptive Representation | Product (Table Outcome) |
$9 \times 1$ | Nine times one | 9 |
$9 \times 2$ | Nine times two | 18 |
$9 \times 3$ | Nine times three | 27 |
$9 \times 4$ | Nine times four | 36 |
$9 \times 5$ | Nine times five | 45 |
$9 \times 6$ | Nine times six | 54 |
$9 \times 7$ | Nine times seven | 63 |
$9 \times 8$ | Nine times eight | 72 |
$9 \times 9$ | Nine times nine | 81 |
$9 \times 10$ | Nine times ten | 90 |
$9\times 11$ | Nine times eleven | 99 |
$9\times 12$ | Nine times twelve | 108 |
$9\times 13$ | Nine times thirteen | 117 |
$9\times 14$ | Nine times fourteen | 126 |
$9\times 15$ | Nine times fifteen | 135 |
$9 \times 16$ | Nine times sixteen | 144 |
$9 \times 17$ | Nine times seventeen | 153 |
$9 \times 18$ | Nine times eighteen | 162 |
$9 \times 19$ | Nine times nineteen | 171 |
| $9 \times 20$ | Nine times twenty | 180 |
Example 1: Calculate 9 times 2 times 1 minus 10
Solution:
9 times 2 times 1 minus 10 can be written as:
$ 9\times2 \times 1 – 10$
$ = 18\times 1 – 10$
$ = 18 – 10$
$ = 8$
Example 2: Find the value of “Y” if “Y x 9 = 81”
Solution:
$ Y \times 9 = 81 $
We know $9\times 9 =91$, so
$ Y = 9 $.
Practice Questions:
- Donald earns 3 dollars in nine days. How much will he earn in 90 days?
- Calculate 3 times 3 times 3?
- From the given table, select the numbers which are multiples of 9
| 17 | 28 | 27 | 18 | 65 |
| 25 | 19 | 11 | 09 | 10 |
| 16 | 81 | 28 | 57 | 95 |
| 30 | 37 | 08 | 13 | 29 |
| 31 | 63 | 70 | 36 | 84 |
| 32 | 44 | 42 | 49 | 80 |
| 72 | 73 | 71 | 74 | 105 |
| 37 | 57 | 56 | 59 | 51 |
| 115 | 82 | 72 | 51 | 65 |
| 49 | 48 | 56 | 89 | 90 |
Answer Key
1) . Donald earns 3 dollars in nine days. We know $9\times 10 = 90$. So, 90 is the tenth multiple of number 9. Total money earned in 90 days would be $3\times 10 = 30$ dollars.
2). 3 times 3 times 3 can be written as:
$ = 3\times 3 \times 3$
$ = 9\times 3$
$ = 27$
3)
| 17 | 28 | 27 | 18 | 65 |
| 25 | 19 | 11 | 09 | 10 |
| 16 | 81 | 28 | 57 | 95 |
| 30 | 37 | 08 | 13 | 29 |
| 31 | 63 | 70 | 36 | 84 |
| 32 | 44 | 42 | 49 | 80 |
| 72 | 73 | 71 | 74 | 105 |
| 37 | 57 | 56 | 59 | 51 |
| 115 | 82 | 72 | 51 | 65 |
| 49 | 48 | 56 | 89 | 90 |
