JUMP TO TOPIC
Construct a Rectangle- Explanation and Examples
 Constructing a rectangle using a compass and straightedge means we construct a space enclosed by two pairs of parallel lines that meet at right angles.
Constructing a rectangle using a compass and straightedge means we construct a space enclosed by two pairs of parallel lines that meet at right angles.
A rectangle is a special kind of parallelogram. It will have opposite sides equal in length. If all four sides have the same length, however, it is also a square.
Todo this, we must be able to construct parallelograms and perpendicular lines. Make sure to review this topic and general rules for construction before moving on.
In this section, we will cover:
- How to Construct a Rectangle
How to Construct a Rectangle
To construct a rectangle, we need to create a quadrilateral that only has right angles. All rectangles have opposites sides that are parallel to each other and equal in length.
If we are given two line segments, AB and CD, we can construct a rectangle with both AB and CD sides of length. Suppose CD is the shorter of the two.
First, we create a line AE perpendicular to AB at A. Then, cut off a segment of AE equal in length to CD. We will call this point F.
Now, we can create two new perpendicular lines. The first will meet AF at a right angle at F. The second will meet AB at a right angle at B. Call the intersection of these lines G.
Now, ABGF is a rectangle with side lengths AB and CD.
Examples
This section will go over common examples of problems involving the construction of a rectangle and their step-by-step solutions.
Example 1
Show that more than one rectangle can be constructed on the line segment AB.

Example 1 Solution
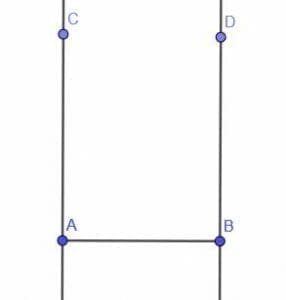
To show that more than one rectangle can include the side AB, we will construct two rectangles.
First, we construct a line AC perpendicular to AB and another line BD perpendicular to AB.
Now, we pick two points at random on AC and call them E and F. Next, we can construct a line perpendicular to AC at E and another at F. We’ll call the intersection of these two lines with BD G and H, respectively.
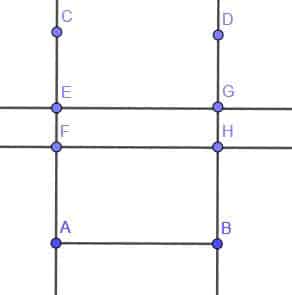
Now, we have two rectangles with the same side, AB, namely ABHF and ABGE.
Note that while this is possible for rectangles, it is not possible for squares.
Example 2
Construct a rectangle whose height is half of its width.
Example 2 Solution
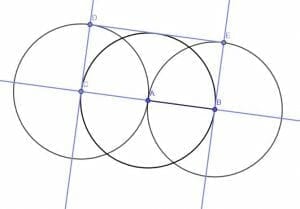
We’ll start this construction similar to the construction for an equilateral triangle.
Construct an infinite line with points A and B on it. Then, construct two circles with radius AB. One will be centered at A and the other at B.
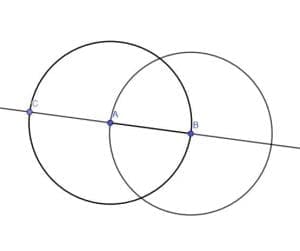
We label the other intersection of the line AB and the circle centered at A with radius AB as C. Note that BC is the circle’s diameter while AB is a radius. That means that BC is twice the length of AB, so that we can use these lengths for our rectangle.
We construct a line perpendicular to AB at C and another a B. Label the intersection of the line perpendicular to AB at B and the circle centered at B with radius AB as E.
Next, we construct a circle with center C and radius CA. Note that CA=AB. We’ll label the intersection of the line perpendicular to AB at C and this circle as D.
When we connect DE, we have a rectangle CBED with a length twice its width.
Example 3
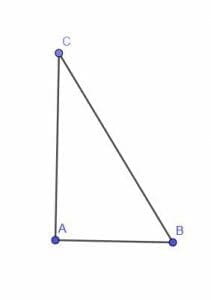
Construct a rectangle whose area is double the area of the right triangle shown.
Example 3 Solution
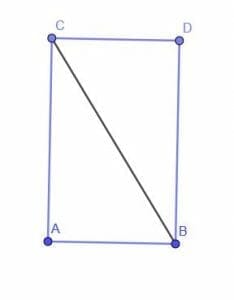
We note that this triangle already has a right angle CAB. We already know that rectangle is a special kind of parallelogram, and we also know that the diagonal of a parallelogram divides it into two equal halves. Therefore, if we construct a rectangle with sides equal to CA and AB, then the rectangle will double the area of the given triangle.
We could do this by copying the angle ACB onto CB. However, an even easier option is to construct a line perpendicular to CA at C and a line perpendicular to AB at B. Call the intersection of these two lines D.
Since CAB, ABD, and DCA are all right angles, BDC is also a right angle. CABD is, therefore, a rectangle with diagonal CB. Thus, its area is twice the area of the triangle ABC, as required.
Example 4
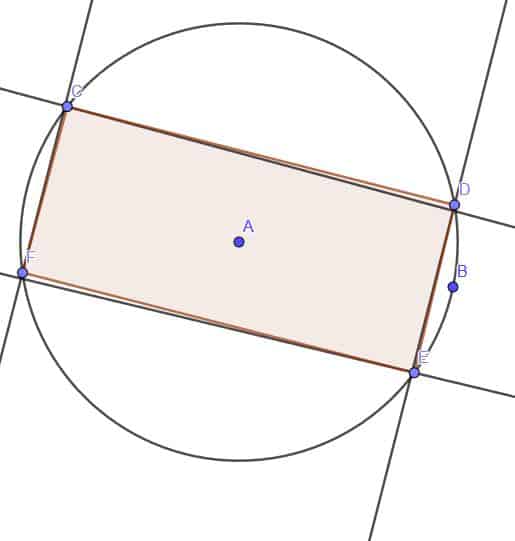
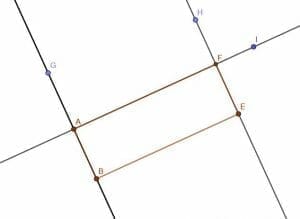
Determine whether or not the following figure is a rectangle.

Example 4 Solution
The figure is clearly quadrilateral as four straight lines enclose it. Therefore, if it has all angles equal to right angles, it is a rectangle. Otherwise, it is some other kind of figure.
We will first extend the line AF to a point I. Then, we can construct a line perpendicular to FI at F, which we will call FH.
The points H, F, and E all lie in the same line, and the points I, F and A all lie in the same line. Since FH and FI are perpendicular by construction, HFI is a right angle. Consequently, its vertical angle AFE is also a right angle.
Likewise, we will construct a line, AG, perpendicular to AF at A. Note that point B also lies on this line. Thus, GAF is a right angle, as is its adjacent angle, FAB.
Finally, we can construct a copy of the segment AB onto EF. These two segments overlap completely and are therefore the same length.
This is enough information to know that this figure is a rectangle.
Example 5
Construct a rectangle with side lengths AB and CD on the line EF.
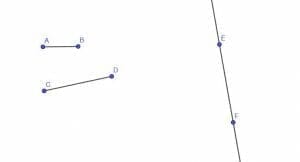
Example 5 Solution
First, we construct a line perpendicular to EF at E. Next, we construct a segment EG equal in length to AB. We can then cut off a segment of the perpendicular line EH equal in length to EG and AB by drawing a circle centered at E with radius EG.
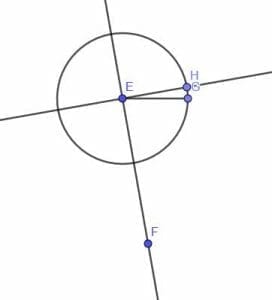
Now, we must cut off a segment on EF equal in length to CD. As before, we’ll construct a segment with endpoint E equal to CD in length. We’ll call it EI.
Next, we construct a circle with center E and radius EI. Label the intersection of this circle and EF as J. EJ will be equal to CD in length.
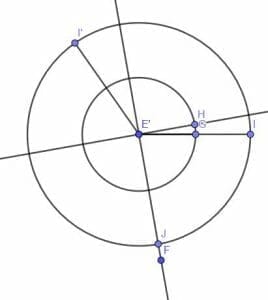
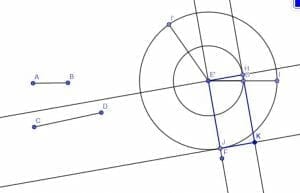
All that’s left then is to construct a line perpendicular to EF at J and another line perpendicular to EH at H. We’ll call the intersection of these two lines K.
Since HEJ, EHK, and EJK are right angles by construction, HKJ must also be right. Thus, HKJE is a rectangle on EF with sides equal to AB and CD’s lengths as required.
Practice Questions
![]()
Open Problems
- Construct a rectangle whose length is three times its width.
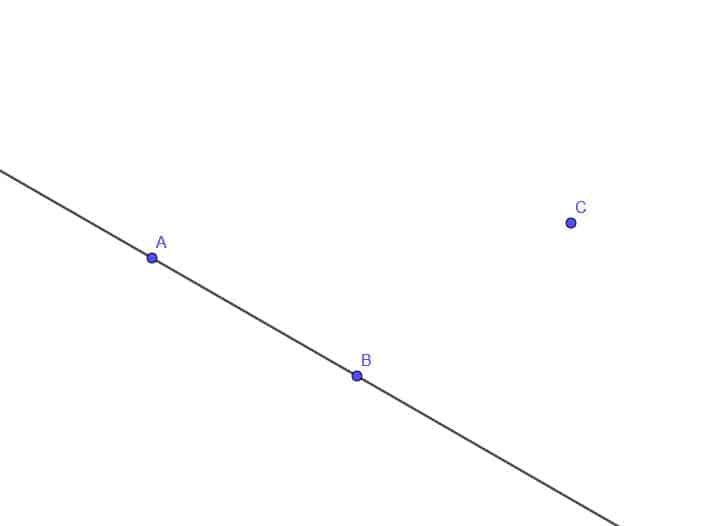
- Construct a rectangle on line $AB$ that has a vertex at $C$.

- Construct a rectangle composed of two $30-60-90$ right triangles.
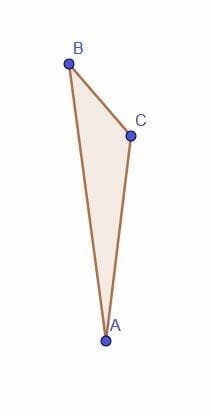
- Construct a rectangle that is twice the area of the scalene triangle $ABC$.

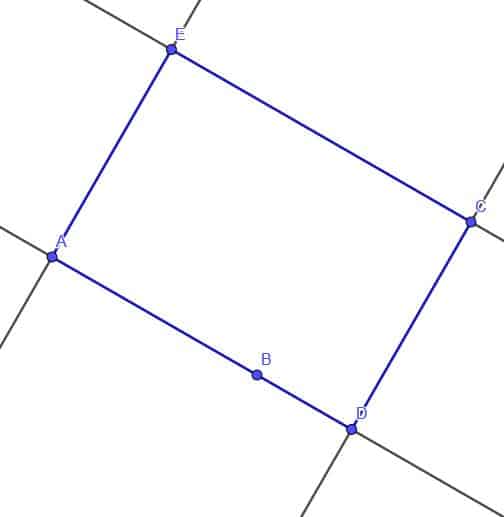
- Determine whether or not the following figure is a rectangle.

Open Problem Solutions



 We know that the triangle $BCD$ has the same area as triangle $BCA$ because $CD$ is an altitude for both. Therefore, the area of each triangle is $\dfrac{1}{2}\cdot BC\cdot CD$. $BCD$ is half of the rectangle $BCDE$, so this rectangle is also double the area of $BCA$.
We know that the triangle $BCD$ has the same area as triangle $BCA$ because $CD$ is an altitude for both. Therefore, the area of each triangle is $\dfrac{1}{2}\cdot BC\cdot CD$. $BCD$ is half of the rectangle $BCDE$, so this rectangle is also double the area of $BCA$.
The perpendicular lines do not line up with the lines of the quadrilateral. Therefore, it is not a rectangle.

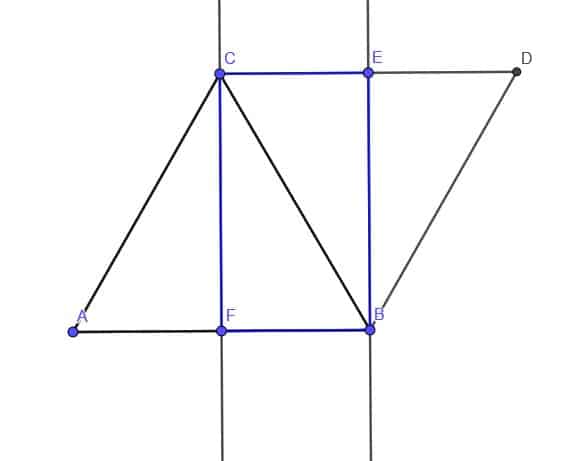
 We know that the triangle $BCD$ has the same area as triangle $BCA$ because $CD$ is an altitude for both. Therefore, the area of each triangle is $\dfrac{1}{2}\cdot BC\cdot CD$. $BCD$ is half of the rectangle $BCDE$, so this rectangle is also double the area of $BCA$.
We know that the triangle $BCD$ has the same area as triangle $BCA$ because $CD$ is an altitude for both. Therefore, the area of each triangle is $\dfrac{1}{2}\cdot BC\cdot CD$. $BCD$ is half of the rectangle $BCDE$, so this rectangle is also double the area of $BCA$.