JUMP TO TOPIC
Construct a Triangle – Explanation and Examples
 It is possible to construct equilateral triangles, isosceles triangles, scalene triangles, acute triangles, obtuse triangles, and right triangles using only a compass and straightedge.
It is possible to construct equilateral triangles, isosceles triangles, scalene triangles, acute triangles, obtuse triangles, and right triangles using only a compass and straightedge.
We have already discussed how to make an equilateral triangle, and we will use this skill to help us make some of the other types of triangles.
Problems involving the construction of triangles include constructing triangles with a giver vertex, a given segment, or three given segments. Construction methods can also help us to classify triangles.
In this topic, we will go over:
- How to Construct a Triangle
- How to Construct a Right Triangle
- How to Construct a Congruent Triangle
- How to Construct a Scalene Triangle
How to Construct a Triangle
Any time we draw a figure enclosed by three straight sides, we construct a triangle. We can classify these figures by the relationship between the lengths of their sides and by the angles the sides form.
Equilateral triangles have three sides of equal length, isosceles triangles have exactly two sides of equal length, and scalene triangles have no sides of equal length. Right triangles have a right angle, obtuse triangles have one angle greater than a right angle, and acute triangles have all three angles less than a right angle. Note that no triangle can have more than one right angle or obtuse angle.
How to Construct a Right Triangle
If we have a right triangle, this means that two of the legs of the triangle are perpendicular. Therefore, to construct a right triangle, we have to construct a line perpendicular to another line. We can then connect any two points on these lines with a straightedge to get a right triangle.
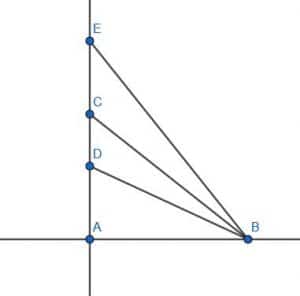
In the figure shown, the lines AD and BC are perpendicular. Therefore, DAB is a right angle. This means that the triangles DAB, CAB, and EAB are all right triangles.
How to Construct a Congruent Triangle
What if we are given a triangle and want to construct another triangle congruent to it?
This is a bit more complicated because it requires us to use several constructions that we have done before.
We must first construct an infinite line DE using any two points in the plane.
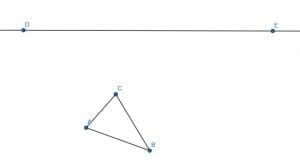
Then, we construct a line segment equal in length to AC with endpoint D. We’ll call this segment DF. After that, we cut off a segment of DE equal in length to AC by constructing a circle with center D and radius DF. We will call the intersection of this circle and DE, G. DG will also be equal in length to AC because it is equal in length to DF, which is equal in length to AC.
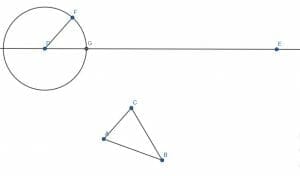
We then similarly construct a segment equal in length to CB on the segment GE, which we will call GH. Finally, we construct a segment HI equal in length to AB.
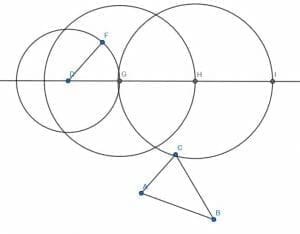
Next, we create a new circle with center G and radius DG. Label the intersection of this circle and the one with center H and radius HI as J. Then, connect GJ and HJ. JHG is congruent to ACB.
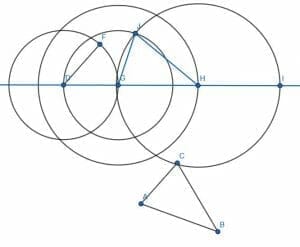
Proof of Congruent Triangles
How do we know that the triangles ABC and JGH are congruent?
We know that DG=AC, GH=CB, and HI=BA. Because they are radii of the same circle, DJ=DG, so DJ=AC by the transitive property. Likewise, because HI and HJ are radii of the same circle, HI=HJ, and HJ=BA. Therefore, the point A lines up with the point J, B lines up with the point H, and C lines up with the point G.
How to Construct a Scalene Triangle
A scalene triangle has all three sides with different lengths.
To construct a scalene triangle, pick three lines that are of different lengths. As above, cut off segments of an infinite line equal in length to the chosen lengths. As before, the three segments should be right in a row.
If the cut segments are AB, BC, and CD, we construct circles with center B and radius AB and with center C and radius CD. Label the intersection of these two circles as E, then connect AE and DE. The triangle AED will have segments equal in length to the original chosen lengths as long as the original lengths satisfied the triangle inequality. Otherwise, the circle with center C and radius CD will not intersect the circle with center B and radius AB.
Triangle Inequality
Suppose we are given three line segments of varying length, AB, CD, and EF. The triangle inequality states that we can construct a triangle with sides equal to the lengths of AB, CD, and EF if and only if:
- AB+CD>EF
- AB+EF>CD and
- EF+CD>AD.
All three of these conditions must be satisfied; otherwise, we cannot construct such a triangle. Stated differently, we can construct a triangle from three segments if and only if the length of any two segments is greater than the third segment’s length.
This requirement is known as the triangle inequality.
Examples
This section will go over common examples involving the construction of triangles and their step-by-step solutions.
Example 1
Construct a right isosceles triangle.
Example 1 Solution
We will first construct a right triangle. Then, we will cut off a segment of the longer side equal to the shorter side’s length.
Begin with a segment, AB. Then, construct the equilateral ABC. Next, construct the angle bisector for ACB. Label the intersection of the bisector and AB as D.
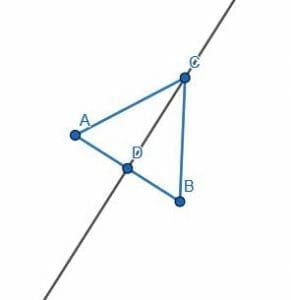
CDB will be a right triangle. Now, we have to cut off a segment of DC, the greater of the two legs that form the right angle, equal to DB’s length, the lesser. To do this, construct a circle centered at D with radius DB. Label the intersection of DC and this circle as E. Since DE is also a radius of the circle, it is equal in length to DB. Therefore, if we construct the segment BE, DBE is an isosceles right triangle.
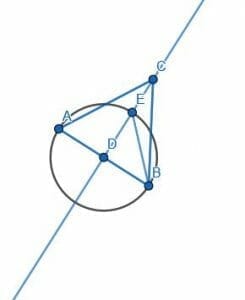
Example 2
Construct an obtuse isosceles triangle.
Example 2 Solution
Let’s return to the construction from example 1, which shows a right isosceles triangle.
We need to construct a new segment, DF, so that FDB is greater than EDB. We also want DF to be equal in length to DB.

Then we can select any point on the circumference of the circle between A and E to be the point F. Then, we connect BF and DF to create the triangle.
In this case, the angle EDB is composed of the two smaller angles EDC and CDB. Since CDB is a right angle, EDC+CDB must be greater than a right angle. Thus, EDB is obtuse, and the triangle EDB is also obtuse.
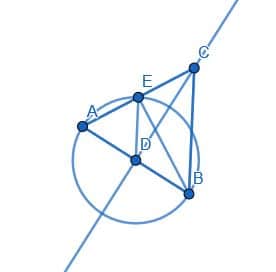
Example 3
Determine whether the following triangle is acute, right, or obtuse.
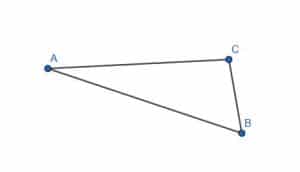
Example 3 Solution
First, we extend the lines AB, BC, and CA to infinite lines.
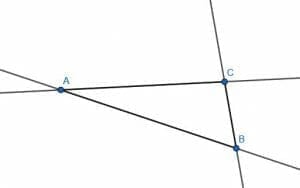
Next, we find a line perpendicular to one of the sides at each vertex. That is, CF is perpendicular to CA, AD is perpendicular to CA, and BE is perpendicular to AB.
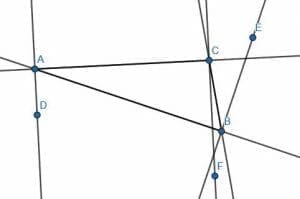
When we consider this figure, we can see how each of the original triangle angles compares to the constructed right angles. The angle CAB lies inside the angle CAD, which is a right angle. Therefore, we know CAB is acute.
Likewise, ABC lies inside ABE. Thus, we know ABC is also acute.
Finally, the angle ACB is composed of the angles ACF and FCB. Since ACF is a right angle, ACF+FCB must be bigger than a right angle. Therefore, we know that ACB is obtuse. Therefore, the whole triangle is obtuse.
Example 4
Show that the segments given do not satisfy the triangle inequality.

Example 4 Solution
We can cut segments of EF equal in length to AB and CD.
Let EG be equal to AB and GH equal to CD. When we do this, we see that H is inside the segment EF. That is, EH is less than EF. Therefore, EF>EH=EG+EH=CD+AB. Thus, the segments CD and AB do not satisfy the triangle inequality.
From this, we know that it is impossible to construct a triangle that has sides of length AB, CD, and EF.

Example 5
Construct a triangle congruent to the given triangle so that the vertex corresponding to A is at the point D.
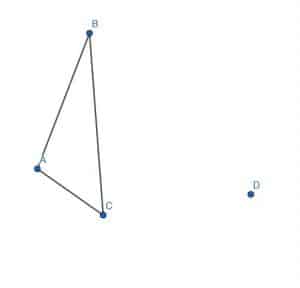
Example 5 Solution
First, we create an infinite line DE, where E is any point in the plane.
Then, we need to construct AB and AC on DE so that each segment has an endpoint at D. We’ll call the segment equal to AB DI and the segment equal to AC DG. We do this to ensure that the point D will line up with the point A when we construct the congruent triangles.
Then, we construct a segment equal to BC to have an endpoint I. We’ll call the other endpoint K.
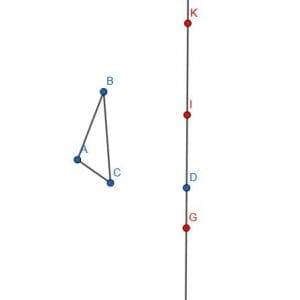
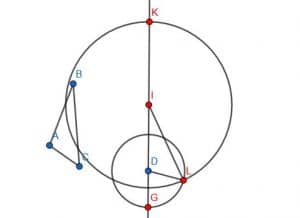
Now, we create two circles. One will have center I and radius IK. The other will have center D and radius DG—label one of the intersections of these circles L.
Now, we can construct the segment DL and IL. The triangle DIL will be congruent to the original triangle ABC.
Practice Questions
![]()
Open Problems
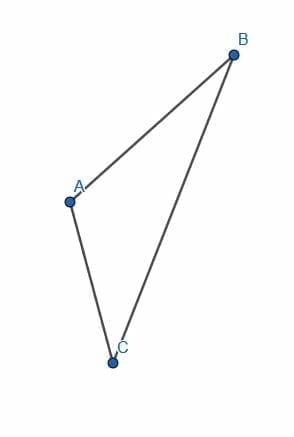
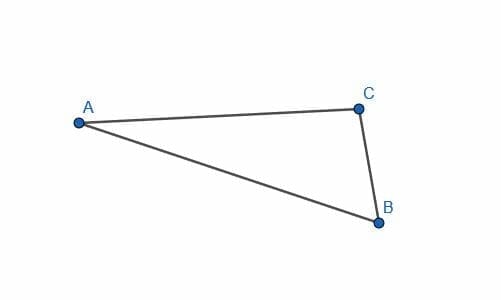
- Show that the triangle $ABC$ is scalene.

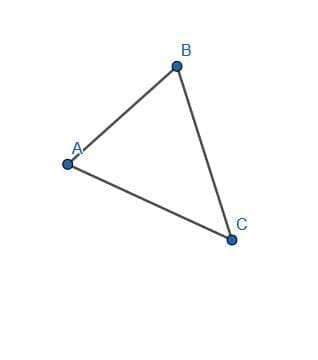
- Classify the triangle $ABC$ as scalene, equilateral, or isosceles.

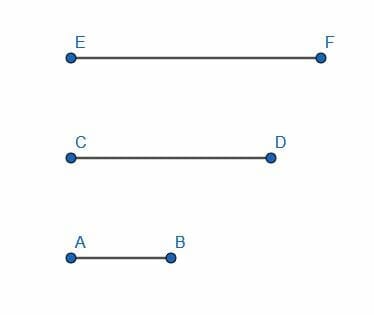
- Show that the segments satisfy the triangle inequality and then construct a triangle from them.

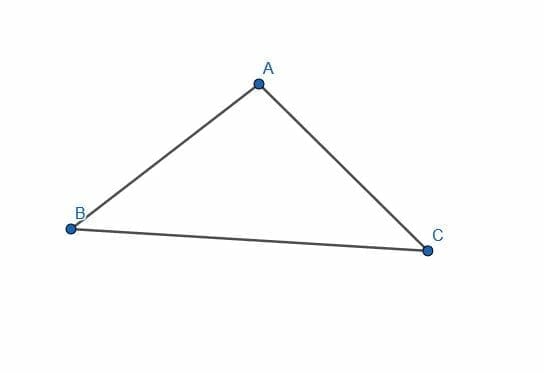
- Construct a triangle congruent to the isosceles triangle $ABC$.

- Construct a triangle congruent to $ABC$ that shares a segment with the original triangle.

Open Problem Solutions
1.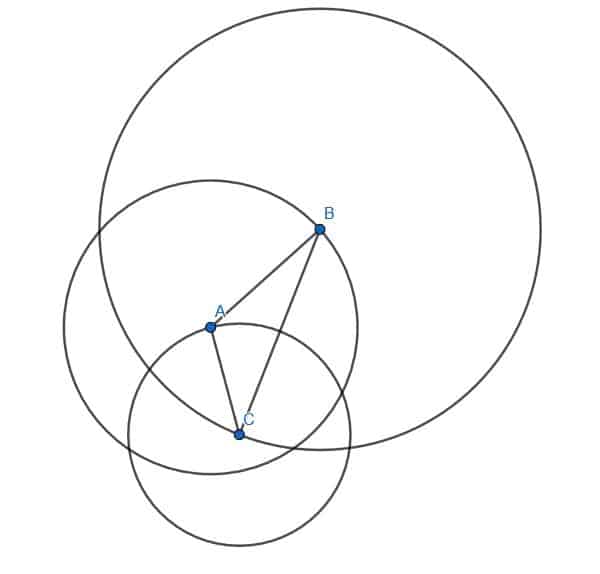
The triangle is scalene. Otherwise, a circle with center $C$ and radius $CA$ would have $B$ on its circumference, and/or a circle with center $A$ and radius $AB$ would have $C$ on its circumference, and/or a circle with center $B$ and radius $BC$ would have $A$ on its circumference.
2.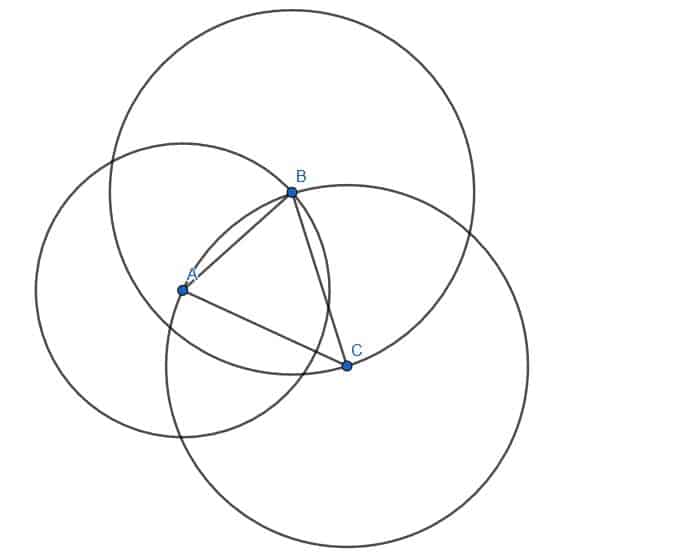
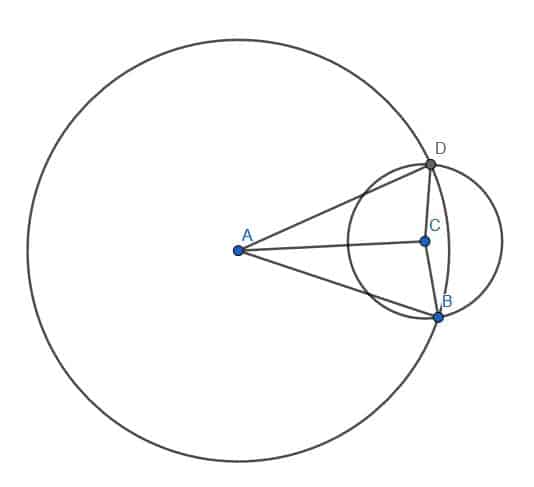
This triangle is isosceles because the circle with center $C$ and radius $CA$ has $B$ on its circumference. Therefore, $AC=BC$.
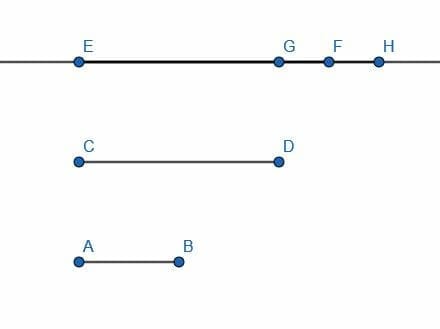
3.
These sides do satisfy the triangle inequality because of $EG=CD$ and $GH=AB$. Together, $EH$ is longer than $EF$, so $CD+AB>EF$ is required.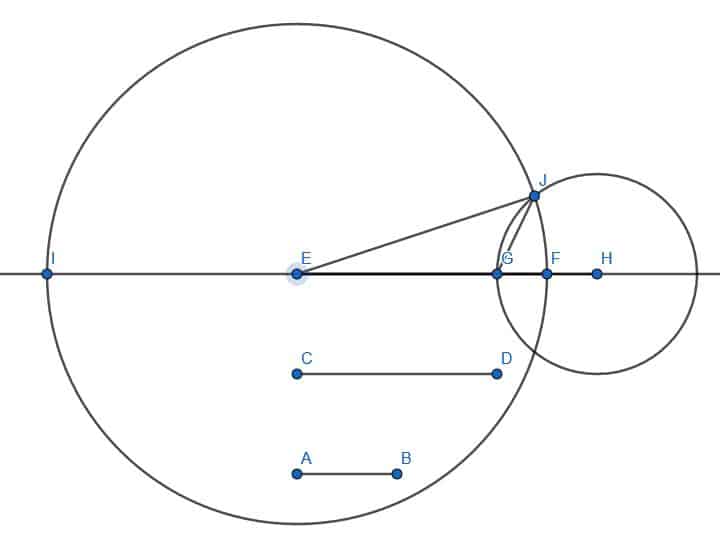
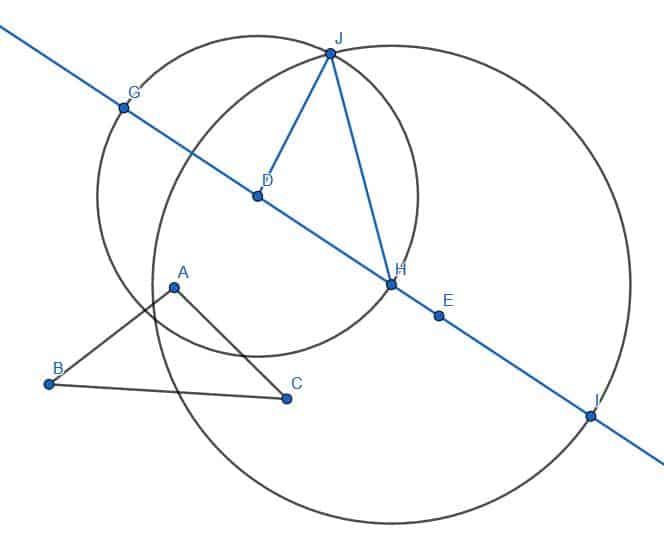
4.
5.
Images/mathematical drawings are created with GeoGebra.