JUMP TO TOPIC
Factors of 40: Prime Factorization, Methods, Tree, and Examples
Factors of 40 are a list of numbers that give a whole number quotient and zero remainders when divided. Or when two numbers are multiplied to produce the number 40, those two numbers will be called the factors of 40.

Figure 1 – All possible Factors of 40
A factor can never be in decimal or fraction form. As the number 40 is an even composite number it will have more than 2 factors. The number 40 has 16 total factors. 8 are positive factors and the rest 8 are negative factors.
This article will let you understand the concept of factors, techniques to calculate the factors, prime factorization, factor tree, factor pair, and its examples.
What Are the Factors of 40?
The factors of 40 are 1, 2, 4, 5, 8, 10, 20, and 40. This means when these numbers divide 40 they produce a whole number quotient and zero remainders.
Note that these factors can also be called the divider since they divide the number 40, which is the dividend, to produce an answer. The list of factors for the number 40 are:
Factors of 40: 1, 2, 4, 5, 8, 10, 20, 40
How To Calculate the Factors of 40?
You can calculate the factors of 40 with two methods:
- Division Method
- Multiplication Method
For the division method you follow these steps:
\[ \dfrac{40}{1}=40\]
\[ \dfrac{40}{2}=20\]
\[ \dfrac{40}{4}=10\]
\[ \dfrac{40}{5}=8\]
\[ \dfrac{40}{8}=5\]
\[ \dfrac{40}{10}=4\]
\[ \dfrac{40}{20}=2\]
\[ \dfrac{40}{40}=1\]
To calculate the factors using the division method you will take the smallest integer i.e 1. Then you will divide the number 40 by 1. Since 1 is a factor of 40 it will you a whole number in the quotient and zero remainders.
To find the list of all of the factors of 40 you will keep on repeating this process for all consecutive integers starting from 1 to 40. As any factor of a number can never be greater than the number itself.
So from the above steps, we can list the factors of 40 as:
Positive factors of 40= 1, 2, 4, 5, 8, 10, 20, 40
Since every number has both positive and negative factors so we can also list the negative factors of 40 as:
Negative factors of 40 = -1, -2, -4, -5, -8, -10,- 20, -40
If you want to find the factors using an alternate method then you will opt for the multiplication method. To find the factors of 40 through this method you will follow these steps:
1 x 40 = 40
In this method, we will multiply any 2 numbers and if the product of these numbers yields 40 then we will consider those numbers as the factors of 40. We will repeat this process until we have multiplied all of the numbers from 1 to 40.
Factors of 40 by Prime Factorization
When the prime factors of any number are multiplied together to give that number then it is called Prime Factorization. As we have already discussed that 40 is a composite number so we can easily find its prime factorization.
To find the prime factorization of 40 we will follow these steps:
\[ \dfrac{40}{2}=20\]
\[ \dfrac{20}{2}=10\]
\[ \dfrac{10}{2}=5\]
\[ \dfrac{5}{5}=1\]
For prime factorization, you will use the smallest prime number that divides the number 40. In this case, it is 2 so we will divide 40 by 2 and the answer will be further divided by 2 until we get a non-decimal number.
Once we get a decimal number we will shift to the next prime number that divides the existing number. We will keep on repeating this process until we get 1 in the answer. We can list all the prime factors like this:
2 x 2 x 2 x 5 = 40
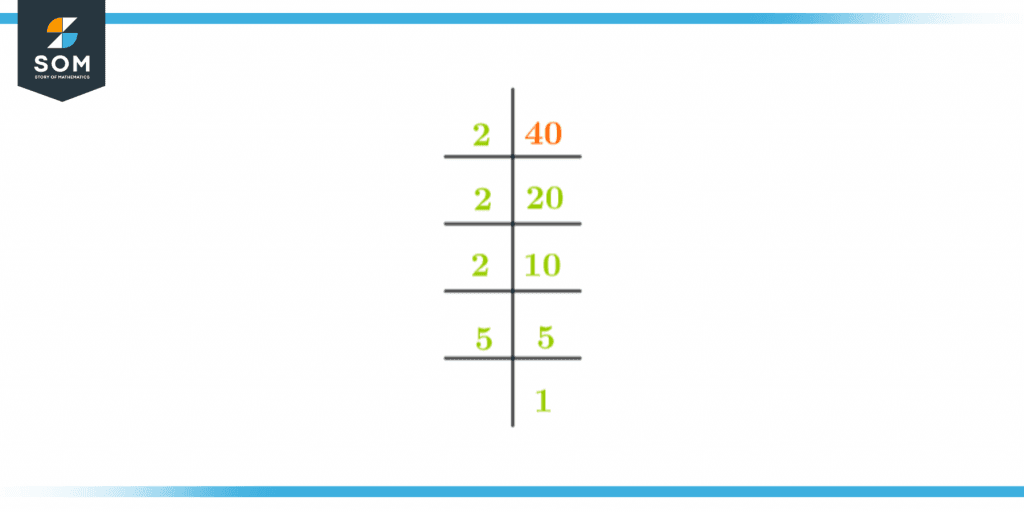
Figure 2 – Prime Factorization of 40
Factor Tree of 40
To demonstrate the prime factors we use a factor tree. At each step, we divide a composite number into its factors and keep on repeating the process until we don’t find a prime number or 1.
The factor tree of the number 40 is as given below:
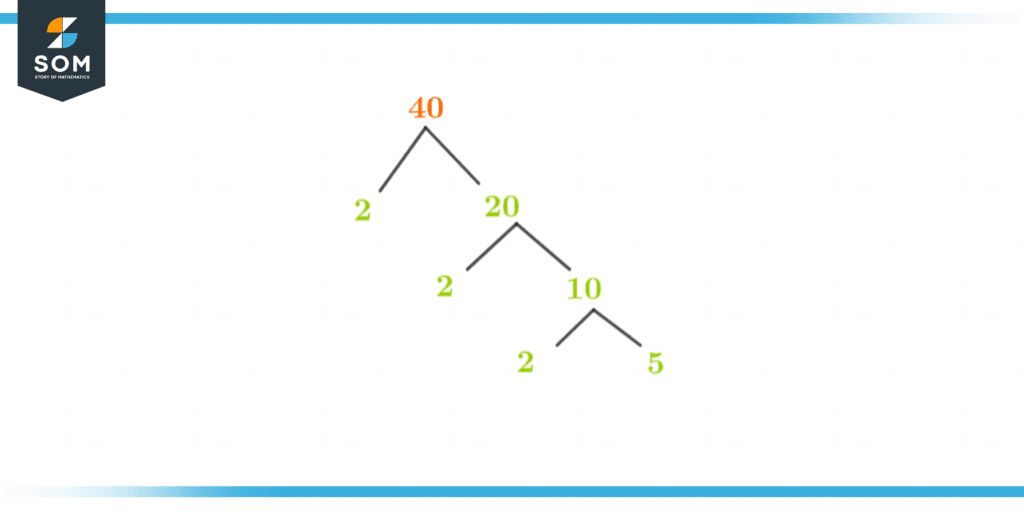
Figure 3 – Factor Tree of 40
Factors of 40 in Pairs
To find the factor pair of the number 40 we multiply any 2 numbers with each other. If the answer of those two numbers is 40 then both the multiplicand and multiplier will be known as the factor pairs of the number 40.
We can list the factor pairs by finding them in this way:
1 x 40 = 40
2 x 20 = 40
4 x 10 = 40
5 x 8 = 40
There is no need to repeat the factors again and again. So the factor pairs of 40 can be written as:
Factor pairs: (1,40), (2,20), (4,10), and (5,8)
Since 40 has both positive and negative pairs so we can also calculate all of the negative pairs:
-1 x -40 = 40
-2 x -20 = 40
-4 x -10 = 40
-5 x -8 = 40
So we can write the negative pair factors as:
Negative Pairs: (-1,-40), (-2,-20), (-4,-10), and (-5,-8).
Factors of 40 Solved Examples
Example 1
Audrey is a music teacher and has been assigned the Christmas choir.
40 children want to participate in this activity. So Audrey must put all of the students in small equal groups in such a way that no one is left behind. Each group must have more than 5 students but less than 10. Can you help Audrey?
Solution
As we know that the Factors of 40 are 1, 2, 4, 5, 8, 10, 20, and 40.
According to this list, we know that the only factor greater than 5 and less than 10 is 8.
So Audrey will make each choir group consisting of 8 children so no one is left out.
Example 2
Write both positive and negative factors of the number 40.
Solution
We can find the factors of 40 by either division or multiplication method. The factors list of the number 40 is as given below:
Factor List of 40 = 1, 2, 4, 5, 8, 10, 20, 40
Similarly, we can find the negative factors of 40 too:
Negative factors of 40 = -1, -2, -4, -5, -8, -10,- 20, -40
Example 3
Calculate the Prime Factorization of the number 40.
Solution
The Prime factorization of 40 can be calculated in this way:
\[ \dfrac{40}{2}=20\]
\[ \dfrac{20}{2}=10\]
\[ \dfrac{10}{2}=5\]
\[ \dfrac{5}{5}=1\]
Hence, we can write it as:
2 x 2 x 2 x 5 = 40
Images/mathematical drawings are created with GeoGebra.
