JUMP TO TOPIC
Factors of -48: Prime Factorization, Methods, Tree, and Examples
The factors of -48 are the numbers that evenly divide -48 with zero remainders. -48 is a negative integer but its factors can be positive as well as negative. It cannot have the positive factor pairs as their product will result in a positive 48. But the factor pairs of -48 can contain 1 positive number and 1 negative number.

Figure 1 – All possible factors of -48
As the laws of multiplication conclude that when a negative number is multiplied by a positive number it results in a negative number. Therefore, one of the factors in the factor pair must be positive, and the other must be negative.
Let’s find out what are the factors of -48 and how to calculate them using various factorization techniques such as prime factorization and division method.
What Are the Factors of -48?
Factors of -48 are 1, -1, 2, -2, 3 -3, 4 -4, 6 -6, 8 -8, 12 -12, 16 -16, 24 -24, 48, and -48. All of these are regarded as the factors of -48 as their product is equivalent to -48.
The factors of -48 can be found using the division and multiplication method. In the division method rules of divisibility are used whereas in the multiplication method factor pairs are found which results in -48 as a product.
How To Calculate the Factors of -48?
You can calculate the factors of -48 by first determining whether it is a composite number or a prime number. Since -48 is a composite number therefore it has more than two factors and can undergo exact division to give a conclusive quotient. The divisor in the division is called the factor of -48.
-48 is also a negative even number. So, it can be divided by 2 as well as -2.
\[ \dfrac{-48}{2} = -24 \]
\[ \dfrac{-48}{-2} = 24 \]
So, 2 and -2 both are the factors of -48 regarded as positive and negative factor.
3 is also divisible by -48 given as:
\[ \dfrac{-48}{3} = -16 \]
\[ \dfrac{-48}{-3} = 16 \]
So 3 and -3 are also the factors of -48.
4 can also be divided by -48 as it is also an even number and the divisibility rule for 4 states that if the last 2-digits of the given number are divisible by 4 then the given number is also divisible by 4. Hence 48 is divisible by 4.
\[ \dfrac{-48}{4} = -12 \]
\[ \dfrac{-48}{-4} =12\]
Therefore, 4 and -4 are the factors of -48.
Coming forward -48 is also the multiple of 6, 8, and 12 therefore it can be divided by 6, 8, and 12 as well leaving nothing behind as a remainder.
\[ \dfrac{-48}{6} = -8 \]
\[ \dfrac{-48}{-6} = 8 \]
\[ \dfrac{-48}{8} = -6 \]
\[ \dfrac{-48}{-8} = 6 \]
\[ \dfrac{-48}{12} = -4 \]
\[ \dfrac{-48}{-12} = 4 \]
Hence 6, -6, 8, -8, 12, and -12 are also the factors of -48.
In a similar manner it can be presumed that all the integers divisible by -48 are the factors.
The remaining factors of -48 are given as:
\[ \dfrac{-48}{16} = -3 \]
\[ \dfrac{-48}{-16} = 3 \]
\[ \dfrac{-48}{24} = 2 \]
\[ \dfrac{-48}{-24} = -2 \]
Lastly, every number has 1 and itself as its factors. Therefore 1, -1, 48, and -48 are also factors of -48.
\[ \dfrac{-48}{1} = -48 \]
\[ \dfrac{-48}{-1} = 48 \]
\[ \dfrac{-48}{48}= -1 \]
\[ \dfrac{-48}{-48} = 1 \]
The factor list -48 is given as:
Factor List: 1, -1, 2, -2, 3 -3, 4 -4, 6 -6, 8 -8, 12 -12, 16,-16, 24 -24, 48, -48
Factors of -48 by Prime Factorization
Prime factorization is the method of calculating prime factors of the given number -48. It is called prime factorization because every factor found using this is a prime number.
The prime factorization of -48 can be done by dividing it by the smallest prime factor which is 2. Upon dividing -48 by 2, -24 is obtained. It can be divided further by 2 to yield 12 as a quotient.
Again further division is possible. Therefore keep dividing it by 2 till 1 is obtained as the result.
The prime factorization of -48 is shown in figure 1 below.
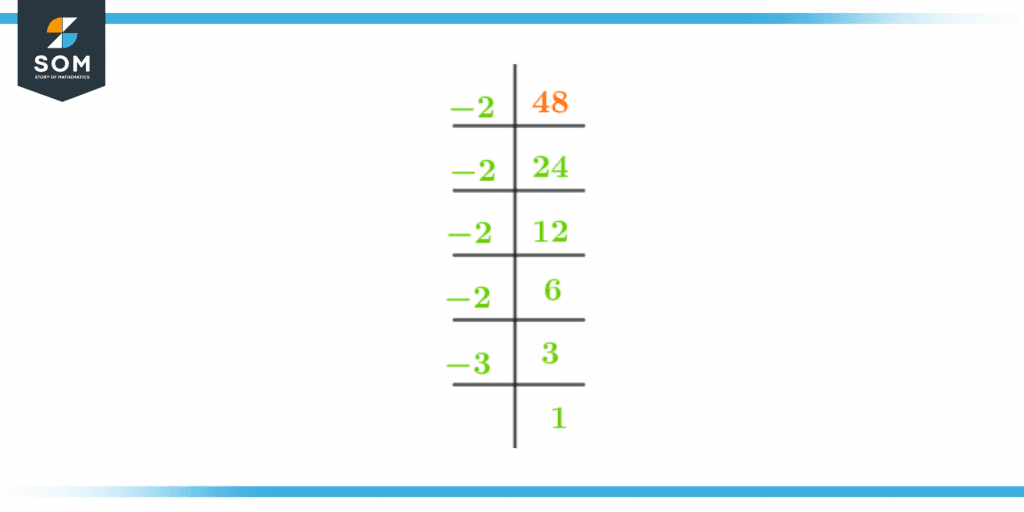
Figure 2 – Prime factorization of -48
Prime Factorization of -48 = -2 x -2 x -2 x -2 x -3
$(-2)^4$ x -3 = -48
Factor Tree of -48
The factor tree method gives us a pictorial representation of the factorization of -48 in terms of its prime factors. It is a way to represent the process of prime factorization. Factor tree comprises prime factors branches and each of them splits into factors of the number.
The branch of the factor tree always stops at the prime number which means that further division is not possible. The factor tree of -48 is shown below in figure 2:
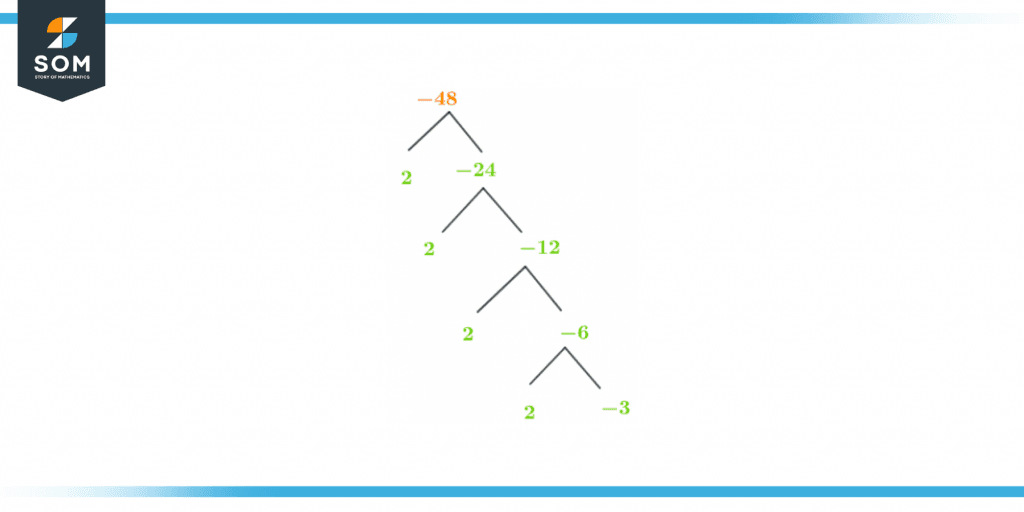
Figure 3 – Factor Tree of -48
Factors of -48 in Pairs
Factors are written in pairs, which when multiplied together result in the original number.
The factor pairs of -48 are as follows:
1 x -48 = -48
2 x -24 = -48
3 x -16 = -48
4 x -12 = -48
6 x -8 = -48
Therefore the factor pairs of -48 are the following:
(1, -48)
(2, -24)
(3, -16)
(4, -12)
(6, -8)
The factor pairs can also be written as:
-1 x 48 = -48
-2 x 24 = -48
-3 x 16 = -48
-4 x 12 = -48
-6 x 8 = -48
Therefore the factor pairs are:
(-1, 48)
(-2, 24)
(-3, 16)
(-4, 12)
(-6, 8)
Factors of -48 Solved Examples
Let’s solve some examples involving the factors of -48.
Example 1
Find the range of the factors of -48.
Solution
The factors of -48 are given as -48 -1, -2, -3, -4, -6, -8, -12, -16, -24, -48, 1, 2, 3, 4, 6, 8, 12, 16, 24, 48.
For finding the range write all these numbers in ascending order.
So the given list becomes:
Ascending Order = -48, -24, -16, -8, -6, -4,
-3, -2, -1, 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
The formula for the range is given as:
Range =largest value – smallest value
Range =48 – (-48)=96
Example 2
Find the median of the positive factors of -48.
Solution
As there are 10 positive factors of -48, the median can be found as the sum of all factors divided by the total number of factors.
\[Median= \dfrac{1 + 2 + 3 + 4 + 6 + 8 + 12 + 16 + 24 + 48}{10} = 12.4 \]
Images/mathematical drawings are created with GeoGebra.
