Factors of 20: Prime factorization, Methods, Tree, and Examples

The factors of 20 are all the numbers, which when multiplied together, their answer is 20. They can also be called numbers that when divided with a specific number give zero as a remainder and the answer is always an integer.

Figure 1 – All possible Factors of 20

Thus, factors of a number are the numbers that are completely divisible by the number itself. You can either choose to multiply or divide numbers to find factors of a specific number. The good thing is that both methods are super easy and are not time taking at all! Factors of 20 will always be the numbers between 1 to 10 as it is a matter of fact that the factors have to be either less than or half the number. When you hear the word “Factor pairs,” always keep in mind that they are the number pairs that can be found through division. A fun fact about the number 20 is that it is the smallest primitive abundant number. When a number is divided with another number and the remainder is 0 and the answer is in the whole number, both the divisor and quotient are to be considered as factors and will be called factor pairs. Factor pairs can be negative and positive. Though, the method of finding factors is the same for both. You just have to reverse the signs. On the other hand, if we write 20 as a product of all its factors it is called “Prime Factorization.”Let’s look at a little example of how to make a factor pair:

2 x 20 = 10

In the following article, we will comprehensively learn about how to find the factors of the number 20. Not just this, you’ll also get to read about what a factor tree is and how we can find the factors of this number through prime factorization. Let’s wait no more and get started.

What Are the Factors of 20?

The number 20 has 6 factors that are 1, 2, 4, 5, 10, and 20. Each of these numbers gives zero as the remainder when divided by 20. So, in total, the number 20 has a total of 6 factors which all give zero as a remainder when 20 is divided from them.

How To Calculate the Factors of 20?

You can calculate the factors of 20 by two easy methods – by division or multiplication. You first should see if a number is prime or composite. A prime number is one that only has two factors, 1 and the number itself.Though, the number 20 is composite as it has 6 factors in total. Write down the numbers that are supposed to be factored in and write down half of it as well. The half of 20 is 10 which means you have to start dividing the numbers between 1 to 10. Each number that is completely divisible by 20 will be called a factor of 20. A few other things you must take care of when opting for the division method is that numbers that when divided give answers in decimals or fractions, can never be called factors. However, negative integers are factors. Before we move on to the other method let’s take an example by dividing the number 20 by two random numbers 2 and 3:\[ \frac {20}{2} = 10 \]\[ \frac {20}{3} = 6.666.. \]As seen from the above example, it is clear that 2 is a factor of 20 whereas 3 is not as the answer to it being divided with 20 is in decimals and it gives off a remainder.Getting factor pairs of numbers is also as easy as determining the factors of a number. You have to keep dividing the specific number i.e. 20 with numbers between 1 to 10. All the possible divisions of the factors of 20 are mentioned below:\[ \frac{20}{1} = 20 \]\[ \frac{20}{2} = 10 \]\[ \frac{20}{4} = 5 \]Thus, the factors of the number 20 are:Factors: 1, 2, 4, 5, 10, 20 In addition to this, every number has negative factors as well. Factors refer to the number that when divided with the number, gives no remainder answering a whole number. If both the features are not present when division is done, neither the divisor nor the quotient will be considered a factor of 20. Most of you might already know about the fun fact that 2 is a factor of all even numbers and 20 is an even number as well. Even numbers are the numbers that can be divided into two halves equally. Thus, if we divide 20 by the number 2 the answer will be 10 and it will give 0 as the remainder, in this case, both 2 and 10 will be considered as the factors of this number and they will also be called a factor pair.

Factors of 20 by Prime Factorization

Prime factorization is a way of writing down a specific number as the product of its prime factors. You can find the factors of 20 by prime factorization in just a few simple steps. In simple words, you just need to keep breaking down the number in the quotient while dividing. This same thing has to be done till we get 1 as the answer. To prime factorize the number 20, you first have to check its smallest prime number i.e. 20. However, the number can also be prime factorized as a product of 4 and 5 (make sure to check if the numbers are prime). As the number 4 is not a prime number it is supposed to be broken down which will eventually be 2 multiplied by 2. Moving on as 5 is a prime number it doesn’t have to be factored any further. So in conclusion the prime factorization of 20 would look like this:\[ \frac{20}{2} = 10 \]The same process will be continued till we get 1 as the answer.\[ \frac{10}{2} = 5 \]\[ \frac{5}{5} = 1 \]The prime factorization of 20 also confirms that 2 is a prime factor of 20. The above-mentioned prime factorization can be written as:

$2^{2}$ x 5 = 16

The prime factorization of the number 20 can also be seen in the diagram shown below: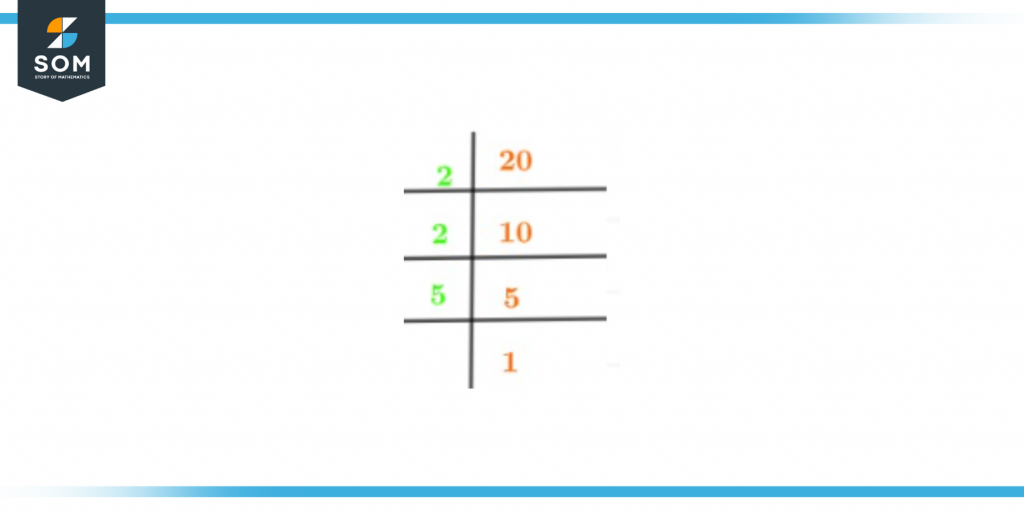

Figure 2 – Prime Factorization of 20

Factor Tree of 20

You can express the products of a specific number as prime factors in various ways. Another way to represent the factors of a number is by making a Factor Tree. Factor trees are made by splitting the factors into 2 branches after every number that can be factored further. Once a number can’t be factorized any further the factor tree comes to an end. The last number on the branch of a factor tree is always supposed to be a prime number, not just for 20 but for every number. According to prime factorization, 2 and 5 are the numbers considered prime factors of the number 20. But as they can be simplified till we get 1 as the answer, thus 1 will be the last number on the factor tree of 20. You can see the diagram of the factor tree of the number 20 below: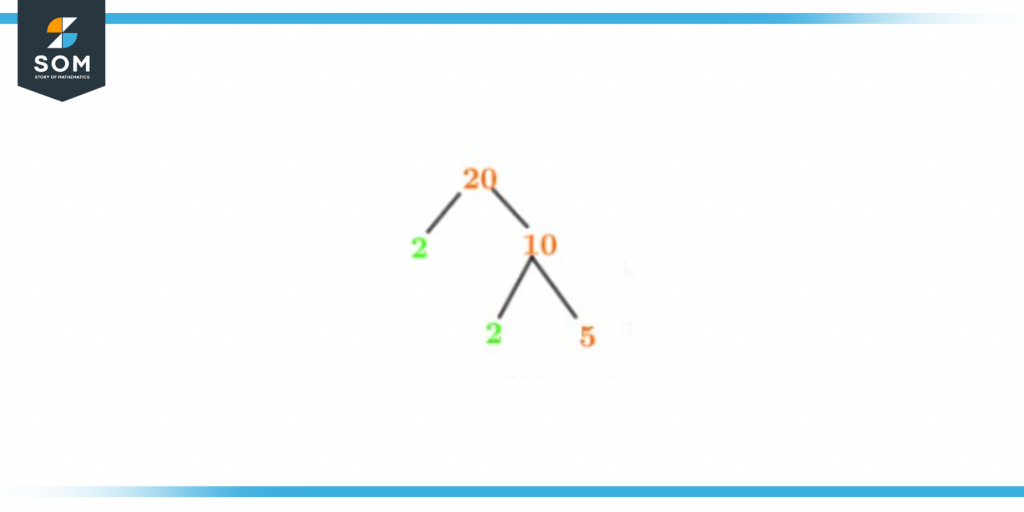

Figure 3 – Factor Tree of 20

Factors of 20 in Pairs

Factor pairs are made when a specific number is divided by other numbers and as a result, we get the answer in whole numbers and the remainder is always zero. The divisor and the quotient of the division taking place are the two numbers that make up the factor pairs.As of now, we are aware of the fact that factors of 20 can be negative and positive both thus if you have the positive factor pairs, you just need to reverse their signs to ‘-’ to get the negative pairs. To find factor pairs step number one is to find all the factors of 16. You can find them by any one of the methods mentioned at the start of this article.Once you have found all the factors by multiplication or division method, the next step is to start multiplying them with each other. The numbers that will give 20 as the answer will be considered as factor pairs as well! The factor pairs of 20 are (1, 20), (2, 10), and (4, 5).

Factors of 20 Solved Examples

To further strengthen the concept of the factors of 20, let’s deal with some of the examples concerning the factors of 20.

Example 1

Find the common factors of 20 and 22.

Solution

To find the common factors of a number, first list down all the factors of both the mentioned numbers. The factors of 20 will be between 1 and 10 whereas, the factors of 22 will be between 1 and 22. Factors: 1, 2, 4, 5, 10, 20 Whereas the factors of 22 are:Factors: 1, 2, 11, 22 Once you’re done listing the factors out, either cancel the uncommon numbers or just circle out the common factors of the two numbers. Thus, the common factors of the numbers 20 and 22 are 1 and 2.All images/mathematical drawings are made by using GeoGebra.