JUMP TO TOPIC
Factors of 21: Prime Factorization, Methods, and, Examples
Factors of 21 are all positive, negative, and whole numbers that may be divided evenly into 21.
Amazingly, dividing 21 by a factor of 21 will result in another factor of 21. Therefore, these can be stated as single factors or as paired factors. In this scenario, we present them in both forms. This usually involves the mathematical breakdown of a certain number.

Figure 1 – All possible Factors of 21
As we know that 21 is not a prime number, it can be divided by other prime numbers. We would need to identify both the positive and the negative factors of 21 to determine the pair factors of 21.
A simple technique to find the factors of any number, in this case, 21, is to check with numbers from 1 to half of that number. Factors are the numbers that are less than or equal to the number itself.
Dividing a number yields the factors of that number, which is another simple method. The quotient and the divisor both function as factors if, at any point during the division of the number 21, the remainder turns out to be 0.
In this article, we will give you the definition of Factors of 21, demonstrate how to find Factors of 21, give you all of the Factors of 21, explain how many factors 21 consists of, and offer you all of the Factor Pairs of 21.
What Are the Factors of 21?
The factors of 21 are 1, 3, 7, and 21; since each of these divides 21 into equal proportions, there are no leftovers. Therefore, these are called the factors of 21
The numbers that divide 21 exactly without leaving a residual are referred to as its factors. In addition to 1 and 21, 21 has a lot of other factors because it is an even composite number.
How To Calculate the Factors of 21?
The factors of 21 are calculated by discovering and compiling a list of all the factors of 21 then examining every number up to and including 21 and determining which numbers produce an even quotient.
Before calculating all of the factors of 21, One must first learn the procedure and processes for computing the factors.
Naturally, writing down the number 21 and attempting to determine the two numbers that would provide the outcome of 21 constitute the initial stage in this process. either 7 and 3 or 21 and 1. The fact that 3 is a prime number is well known. Examples of prime numbers are 2 and 5.
We can see that the smallest prime integer, 3, divides 21 in this scenario. The result of dividing 21 by 3 gives a quotient of seven. Consequently, both 7 and 3 must be factors of 21. 7 is a prime number as well because it can be divided only by seven and one. The different distinct integers that would be acquired as factors of the number 21 must be written in the last step.
We only need to divide 21 by all numbers up to 21 to see which ones provide an equal quotient because the factors of 21 are all the numbers that you can divide evenly by 21. When we accomplished that, the quotient produced by these calculations is even:
\[ \frac{21} {1} = 21.00\]
\[ \frac{21} {2} = 10.5\]
\[ \frac{21} {3} = 7.00\]
\[ \frac{21} {4} = 5.25\]
\[ \frac{21} {5} = 4.20\]
\[ \frac{21} {6} = 3.50\]
\[ \frac{21} {7} = 3.00\]
\[ \frac{21} {8} =2.63\]
\[ \frac{21} {9} = 2.33\]
\[ \frac{21} {10} = 2.10\]
\[ \frac{21} {11} = 1.91\]
\[ \frac{21} {12} = 1.75 \]
\[ \frac{21} {13} = 1.62\]
\[ \frac{21} {14} = 1.50\]
\[ \frac{21} {15} = 1.40\]
\[ \frac{21} {16} = 1.31\]
\[ \frac{21} {17} = 1.24\]
\[ \frac{21} {18} =1.17\]
\[ \frac{21} {19} = 1.11\]
\[ \frac{21} {20} = 1.05\]
\[ \frac{21} {21} = 1.00\]
Therefore, all the integers we divided (used as divisors earlier) to arrive at an even number by rejecting the decimals are the positive factors of 21. The full list of Positive Factors of 21 is presented below in numerical order:
1, 3, 7, and 21.
Negative numbers are also factors of 21. All of the positive factors in the number 21 can therefore be changed to negative numbers. The list of the 21 negative factors includes:
Negative factors of 21 = -1, -3, -7, and -21.
How Many Factors of 21 are There?
When we compile all the factors that makeup 21, we discovered that there are four positive and four negative factors; thus, there are eight factors of 21 in all.
Factors of 21 by Prime Factorization
The prime factorization of 21 is given as 3×7.
First, keep in mind that all positive integers considered to be prime numbers may only be divided equally by one and by oneself. All prime numbers that when multiplied together, equal 21, are known as prime factors of 21.
Prime Factorization of 21 is the process of locating the prime factors of 21. You must divide 21 by the smallest prime number feasible to obtain the prime factors of 21. The next step is to divide the outcome by the smallest prime integer. Continue doing this until you have 1.
The arithmetic to demonstrate is as follows:
\[ \frac{21} {3} = 7\]
\[ \frac{7} {7} = 1\]
Once more, the prime factors of 21 are all the prime numbers you used to divide above. The 21 prime factors are as follows: (3, 7)
The prime factorization of 21 is shown below in Figure 1:
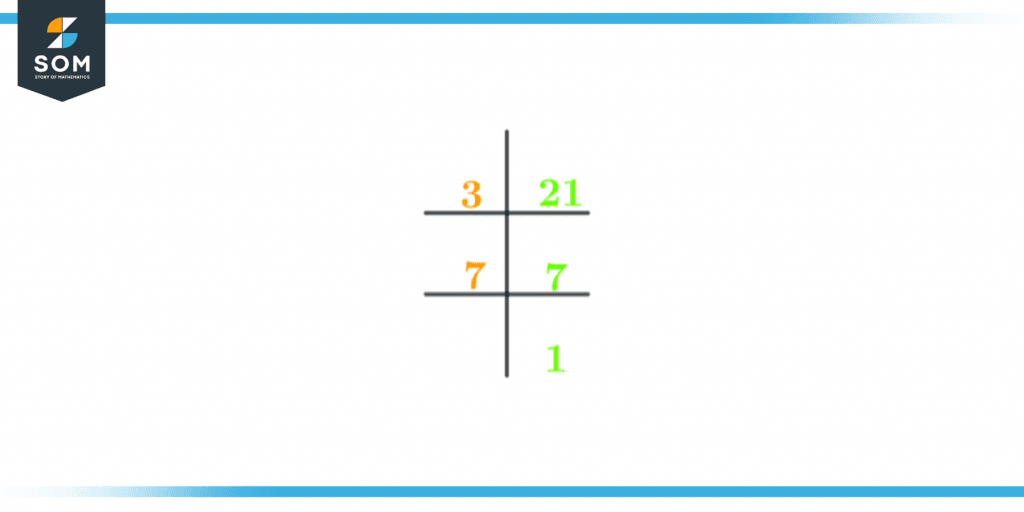
Figure 2 – Prime factorization of 21
We discover that 21 has a total of 2 prime factors when we tally the number of prime factors mentioned above.
Factor Tree of 21
The factor tree of 21 is given below in figure 2:
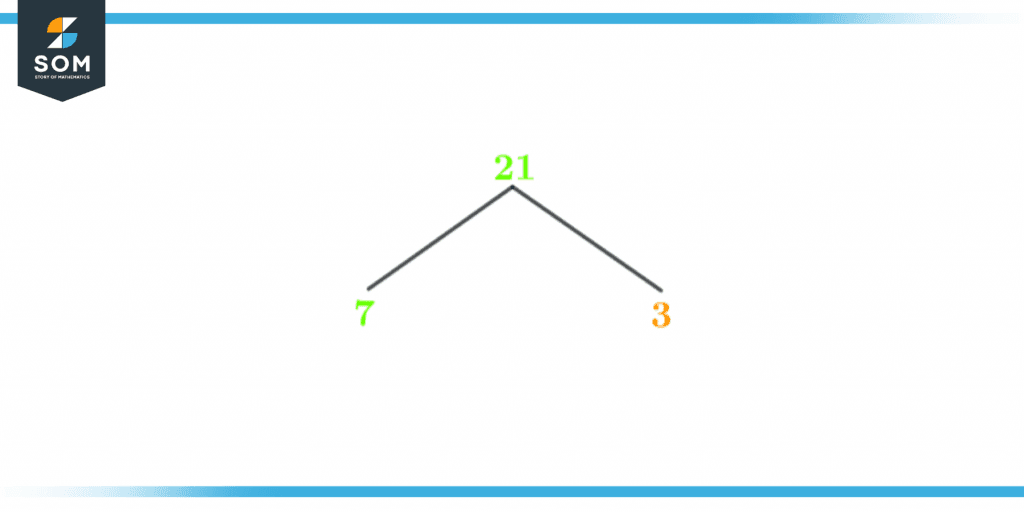
Figure 3 – Factor tree of 21
The Factor Tree is just one of several representations that can be used to show the factors of a given integer. Any number’s prime factors are shown graphically in the number’s factor tree.
A factor tree is a visual representation of a number’s potential factors and their corresponding sub-factors. It is intended to make factorization simpler. It is made by first determining the factors of a number, and then the factors of the original number.
The procedure is repeated again and again until you have obtained a sufficient number of prime factors, which is the prime factorization of the initial integer. Always keep in mind the second component of a factor pair when building the tree.
Factors of 21 in Pairs
A factor pair of 21 is a pair of factors that when multiplied together, results in 21. The number 21 is known as the product in mathematics, and the two numbers that can be multiplied together to equal it are known as the factors.
We must first obtain all of the factors of 21 before we can calculate the factor pairs of 21. Once you have a list of every one of those factors, you can pair them together to create a list of every pair of factors.
As we are aware of every factor that contributes to the number 21, we can utilize this knowledge to determine the factor pairings. To do this, we may search through the list of possible combinations to multiply with each other to find all the possible combinations of 21.
21 x 1 = 21
7 x 3 = 21
3 x 7 = 21
1 x 21= 21
Factors of 21 include negative values, as we mentioned earlier. You may convert the list of positive factor pairs above to negative factor pairs of 21 by simply adding a minus sign in front of each factor. Minus times minus becomes positive.
The positive factor pairs of the number 21 are (21, 1) and (3, 7). The negative pair factors of 21 are (-21, -1) and (-3, -7).
Factors of 21 Solved Examples
Example 1
What are the common Factors of 21 and 84?
Solution
First Write down all the factors of 21 and 84.
The list of all the factors of 21 is 1, 3, 7, and 21.
List of all the factors of 84 are:1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, and 84.
Now find the factors that are common in both 21 and 84, those will be the common factors of 21 and 84.
So the common factors between 21 and 84 are 1, 3, 7, and 21.
Example 2
Find the greatest common factor between 21 and 126.
Solution
First, list down factors of 21 and 126.
The list of all factors of 21 are 1, 3, 7, and 21 and the factors of 126 are 1, 2, 3, 6, 7, 9, 14, 18, 21, 42, and 63.
The common factors between 21 and 126 are 1, 3, 7, and 21 and from these the greater common factor is 21.
Therefore the greatest common factor between 21 and 126 is 21.
Images/mathematical drawings are created with GeoGebra.
