JUMP TO TOPIC
Factors of 224: Prime Factorization, Methods, Tree, and Examples
The Factors of 224 is the list of all possible positive and negative whole numbers that you can divide evenly by 224.

Figure 1 – All possible factors of 224
A factor of 224 when divided by 224 will result in another factor of 224. 224 is a three-digit even number. It has multiple factors like 1,2,4,7,8, 14, etc. The total number of factors number 224 is 12.
224 is also a Composite Number. Composite numbers refer to those numbers that have more than two factors unlike prime numbers,
which only have two factors, the number itself and the number 1 which is the factor of every natural number.
Let us explore how to find the factors of 224, what is the prime factorization of 224 and how to draw its factor tree.
What Are the Factors of 224?
The complete factors of 224 are 1, 2, 4, 7, 8, 14, 16, 28, 32, 56, 112, and 224.
Numbers that divide 224 perfectly and leave 0 as the remainder are known as its factors. Therefore, the method for discovering and compiling a list of all the factors of 224 is to examine every number up to and including 224 and determine which numbers produce an even quotient (which means no decimal place).
How To Calculate the Factors of 224?
You can find the factors of 224 by dividing it by the list of natural numbers from 1 to 224. The natural numbers that will divide 224 completely without leaving any remainder will be regarded as the factors of 224.
Firstly, divide 224 by 1 which is the smallest natural number.
\[ \dfrac{224}{1} = 224 \]
Since the remainder is zero, therefore, 1 is the factor of 224.
Now, split 224 in half that is 112, and keep on dividing 224 by the numbers till 112. The numbers that will produce zero remainders as the divisors are the factors of 224.
The numbers that will give zero remainders are the following:
\[ \dfrac{224}{2} = 212 \]
\[ \dfrac{224}{4} = 56 \]
\[ \dfrac{224}{7} = 32 \]
\[ \dfrac{224}{8} = 28 \]
\[ \dfrac{224}{14} = 16 \]
\[ \dfrac{224}{16} = 14 \]
\[ \dfrac{224}{28} = 8 \]
\[ \dfrac{224}{32} = 7 \]
\[ \dfrac{224}{56} = 4 \]
\[ \dfrac{224}{212} = 2 \]
Therefore, all of the above numbers are divisible by 224 and are called factors of 224.
224 is also the factor of 224 as every number is a factor of itself as well.
\[ \dfrac{224}{224} = 1 \]
The factor list of 224 is given as:
Factors of 224 = 1, 2, 4, 7, 8, 14, 16, 28, 32, 56, 112, 224
Important Properties
Here are some important points regarding factors of 224 that must be noted:
- 224 is an even number having both even and odd factors.
- The factors of 224 can be determined using the rules of divisibility.
- None of the factors of 224 is in the form of decimal or fraction.
- The negative factors of 224 are the additive inverse of its positive factors.
- The sum of all the factors 224 is 504.
- Factors of 224 can be found using both the prime factorization and rules of divisibility technique.
Factors of 224 by Prime Factorization
Prime Factorization of 224 is the process of locating the prime factors of 224. By
dividing 224 by the smallest prime number attainable, you may get the prime factors of 224. The next step is to divide the outcome by the smallest prime integer. Continue doing this until you have 1.
All those positive integers are classified as prime numbers that can only be divided equally by 1 and by themselves. All prime numbers that when multiplied
together, equal 224 are known as prime factors of 224.
The prime factorization of 224 is shown below in figure 1:
The process of prime factorization starts by dividing 224 by its largest prime factor which is 7. Then divide it by 2 and continue the process till 1 is received as the quotient.
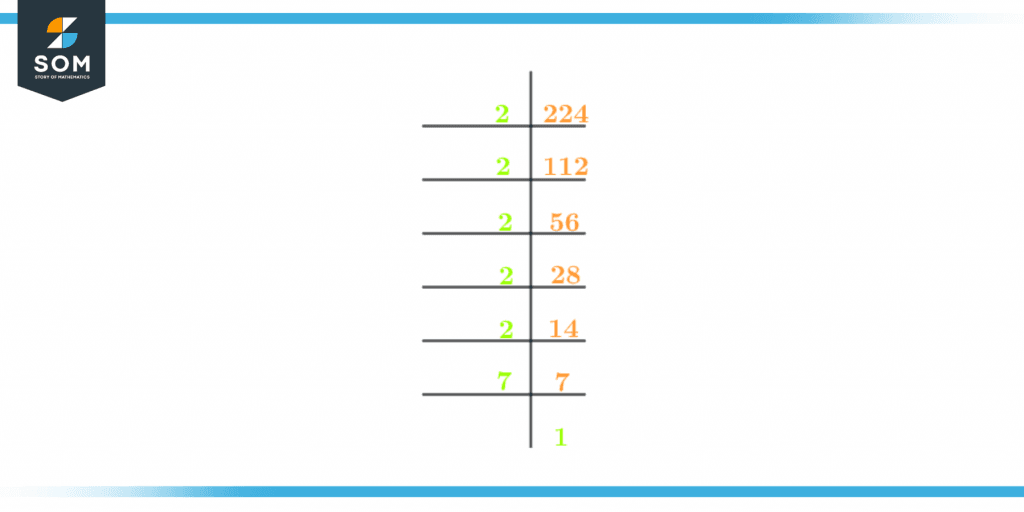
Figure 2 – Prime factorization of 224
The Prime factorization of 224 can also be expressed as:
$2^{5}$ x 7 = 224
The difference between prime factorization and the division method is that the numbers are expressed as the product of prime factors when using the prime factorization method. In contrast, when using the division method, the given integers are divided by the least common multiple until there are zero remainders.
Factor Tree of 224
A factor tree is the pictorial description of the prime factorization of a particular number. It includes all the prime factors of the number.
The factor tree splits branches into numbers divisors and quotients and continues till the remaining quotient is converted into the lowest form and further division is not possible.
The factor tree of the number 224 is given below in figure 2:
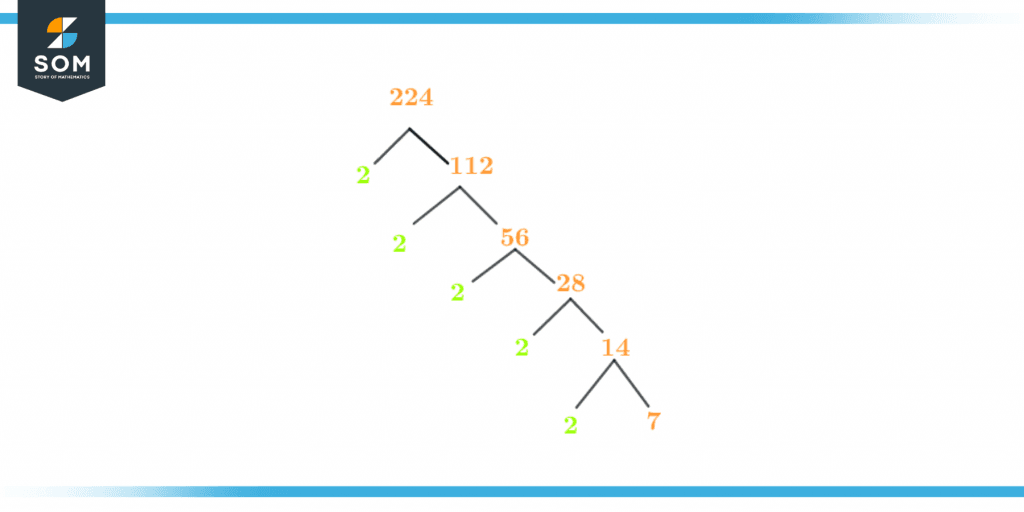
Figure 3 – Factor tree of 224
We discover that 224 has a total of 2 prime factors after counting the prime numbers mentioned above.
The product of 224 prime numbers is obtained by multiplying all the Prime Factors of 224. Prime Factors of 224 as a Product are given as:
2 x 2 x 2 x 2 x 2 x 7 = 224
Factors of 224 in Pairs
A factor pair of 224 is the pair consisting of any two factors that, when multiplied together, results in 224. The number 224 is known as the product, and
the two numbers that are multiplied together to equal it are known as the factors.
We must first obtain all of the factors of 224 before we can determine the factor pairs of 224. Once you have a list of every one of those factors, you can pair them together to create a list of every pair of factors.
Now that we are aware of all the components that contribute to the number 224, we can utilize this information to determine the factor pairs. To do this, we can search through the list of possible combinations to identify the factors that add up to 224.
The factorization of 224 is given as:
1 x 224 = 224
2 x 212 = 224
4 x 56 = 224
7 x 32 = 224
8 x 28 = 224
14 x 16 = 224
Therefore the possible factor pairs of 224 are (224, 1), (112, 2), (56, 4), (32, 7), (16, 14), and (28, 8).
Factors of 224 Solved Examples
Let us solve some examples involving the factors of 224.
Example 1
What are the common factors of 224 and 56?
Solution
First list down all the factors of 224 and 56.
A list of all the factors of 224 is:
Factor List of 224 = 1, 2, 4, 7, 8, 14, 16, 28, 32, 56, 112, 224
A list of all the factors of 56 is:
Factor List of 56 = 1, 2, 4, 7, 8, 14, 28, 56
Now, find the factors that are common in both 224 and 56, those will be the common factors of 224 and 56.
So, the common factors between 224 and 56 are 1, 2, 4, 7, 8, 14, and 28.
Example 2
What are the common factors of 224 and 32?
Solution
The factors of 224 are given as:
Factors of 224 = 1, 2, 4, 7, 8, 14, 16, 28, 32, 56, 112, 224
The factors of 32 are given as:
Factors of 32 = 1, 2, 4, 8, 16, 32
The common factors are 1, 2, 4, 8, 16, and 32.
Example 3
List the negative factor pairs of 224.
Solution
When we multiply two negative numbers the resultant is always Positive. So as a result, the pairs of negative factors for 224 are:
(-224, -1), (-112, -2), (-56, -4), (-32, -7), (-16, -14), (-28, -8)
Images/mathematical drawings are created with GeoGebra.
