JUMP TO TOPIC
Factors of 252: Prime Factorization, Methods, Tree, and Examples

Figure 1 – All possible Factors of 252
The factors of 252 are the set of natural numbers which give 252 when multiplied by one another. The two numbers undergoing multiplication constitute a factor pair.
The factors of 252 can also be defined as the set of natural numbers that make the number 252 completely divisible upon them. The only condition is that such numbers are bound to leave zero as the remainder and a whole number quotient to be labeled as “factors.”
The number 252 is an even composite number, which indicates that this number will have more than two factors. These factors can be determined through the division method. If you want to search for specific factors, say prime factors, then the methods are the prime factorization and the factor tree methods.
In this article, we will conduct a detailed evaluation of these multiple methods for determining the factors of 252. We will also solve some examples involving these factors for better understanding.
What Are the Factors of 252?
The factors of 252 are 1, 2, 3, 4, 6, 7, 9, 12, 14, 18, 21, 28, 36, 42, 63, 84, 126, and 252. These natural numbers make 252 completely divisible upon them.
The number 252 has 18 factors in total, and these 18 factors can be evenly split into 9-factor pairs – positive and negative.
How To Calculate the Factors of 252?
You can calculate the factors of 252 by using the division method. As mentioned above, the number 252 is even composite, so it will have multiple factors, 18 precisely.
The division method is the simplest method for determining all these 18 factors. The division method has a simple rule – if the remainder is zero and a quotient is not a decimal number, then it’s a factor.
As the general rule of factors, the number 1 and the number 252 already act as the smallest and largest factors, respectively. Still, since 252 is an even number, the number 2 will also be one of its factors.
Given below is the demonstration of the division method for determining all these factors:
\[ \frac{252}{1} = 252 \]
\[ \frac{252}{2} = 126 \]
\[ \frac{252}{3} = 84 \]
\[ \frac{252}{4} = 63 \]
\[ \frac{252}{6} = 42 \]
\[ \frac{252}{7} = 36 \]
\[ \frac{252}{9} = 28 \]
\[ \frac{252}{12} = 21 \]
\[ \frac{252}{14} = 18 \]
\[ \frac{252}{18} = 14 \]
\[ \frac{252}{21} = 12 \]
\[ \frac{252}{28 } =9 \]
\[ \frac{252}{36} = 7 \]
\[ \frac{252}{42} = 6 \]
\[ \frac{252}{63} = 4 \]
\[ \frac{252}{84} = 3 \]
\[ \frac{252}{126} = 2 \]
\[ \frac{252}{252} = 1 \]
Therefore, the complete list of factors of 252 is:
Factors of 252: 1, 2, 3, 4, 6, 7, 9, 12, 14, 18, 21, 28, 36, 42, 63, 84, 126, and 252
As the number 252 is a natural number and the factor this number has also been set of natural numbers, two possible integers exist – one positive and the other negative. So in the way, negative factors of 252 can also exist, which are the same as the positive ones except with a negative sign.
The negative factors of 252 are:
Negative Factors of 252: -1, -2, -3, -4, -6, -7, -9, -12, -14, -18, -21, -28, -36, -42, -63, -84, -126, and -252
Factors of 252 by Prime Factorization
Prime factorization is the technique used to determine specific factors of a number. These particular factors are known as prime factors. The prime factors are the numbers included in the factor list of a number and are prime numbers.
The prime factorization technique is based on the mathematical operation of division in which only the prime numbers can occupy the place of divisors. These prime numbers carry out the division.
The division through prime numbers is carried out until the last step, indicating that only the number 1 should be reminded at the end as the result of the division.
The prime factorization for the number 252 is shown below:
252 $\div$ 2 = 126
126 $\div$ 2 = 63
63 $\div$ 3 = 21
21 $\div$ 3 = 7
7 $\div$ 7 = 1
By using prime numbers for division, the prime factorization for 252 can be mathematically written in the form of one equation, as shown below:
Prime Factorization of 252 = 2 x 2 x 3 x 3 x 7
Or
Prime Factorization of 252 = $2^{2}$ x $3^{2}$ x 7
The prime factorization is also shown below in the figure:
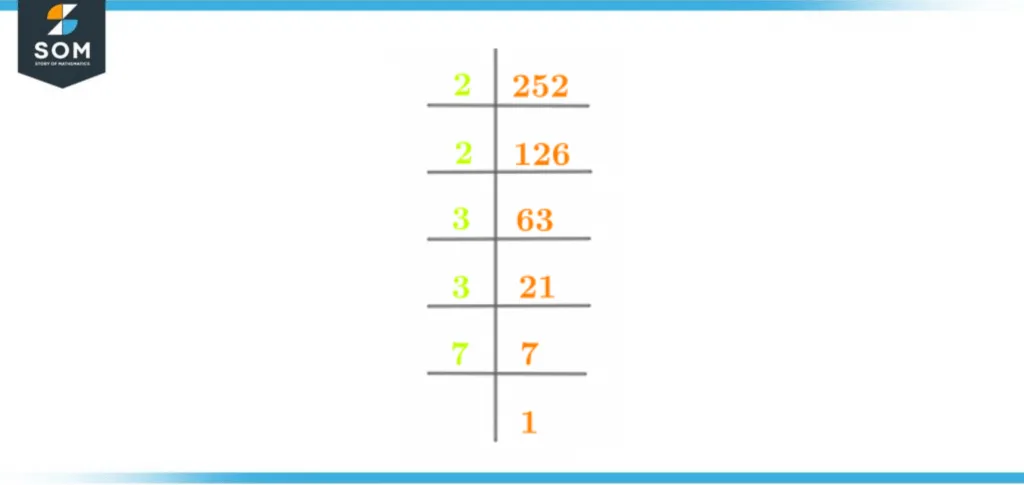
Figure 2 – Prime Factorization of 252
Hence, the prime factors obtained are:
Prime Factors of 252 = 2, 3, and 7
Factor Tree of 252
Like the prime factorization, the factor tree is also used to determine a number’s prime factors. The factor tree represents the prime factors in a visual manner through a tree-like structure.
The factor tree consists of two branches that originate from a number. The factor tree always requires one of these branches to hold a prime number. The other branch has the number which is subjected to division.
The division of numbers continues until the factor tree only holds prime numbers at both branches.
The factor tree for the number 252 is shown below:
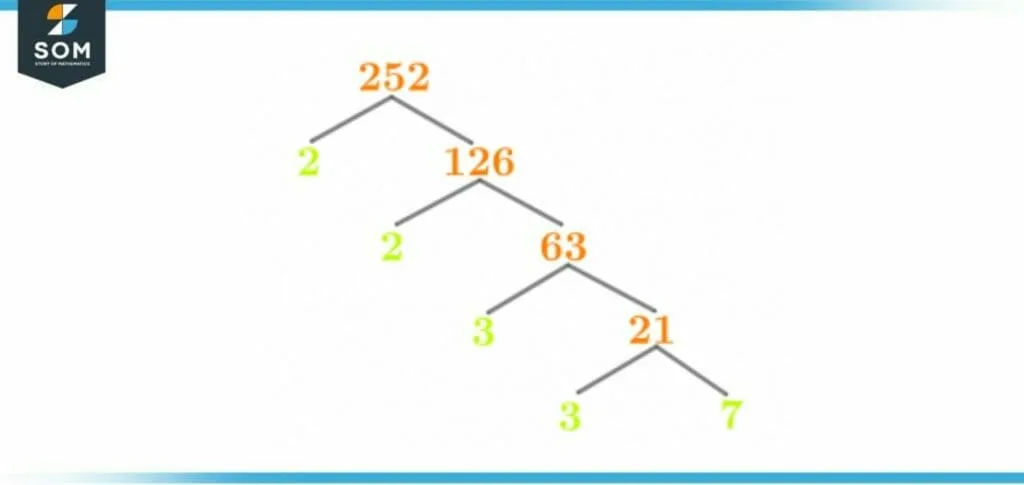
Figure 3 – Factor Tree of 252
Factors of 252 in Pairs
The factors of 252 also have the tendency to exist in the form of pairs known as factor pairs. One factor pair will comprise two numbers that will give the original number as the result when they are multiplied by each other.
The requirement for the factor pair is that both numbers must have the same sign. The number 252 has 18 factors, meaning that this number will have 9-factor pairs. These are given below:
1 x 252 = 252
2 x 126 = 252
3 x 84 = 252
4 x 63 = 252
6 x 42 = 252
7 x 36 = 252
9 x 28 = 252
12 x 21 = 252
14 x 18 = 252
The positive factor pairs of 252 are given below:
(1, 252)
(2, 126)
(3, 84)
(4, 63)
(6, 42)
(7, 36)
(9, 28)
(12, 21)
(14, 18)
As the factors of 252 can also be negative, the same implies to the factor pairs. The negative factor pairs of the number 252 are given below:
Negative Factor Pairs of 252 can be stated as follow:
(-1, -252)
(-2, -126)
(-3, -84)
(-4, -63)
(-6, -42)
(-7, -36)
(-9, -28)
(-12, -21)
(-14, -18)
Factors of 252 Solved Examples
The above sections cover all the details regarding the factors of 252. Now let’s move on to solve solved examples of the factors of 252 that will further enhance our understanding.
Example 1
List down the factors of 252 and separate the even and the odd factors of 252.
Solution
Let’s consider the first part of the example: list down the factors of 252. These factors are given below:
Factors of 252: 1, 2, 3, 4, 6, 7, 9, 12, 14, 18, 21, 28, 36, 42, 63, 84, 126, and 252
Now, let’s separate the odd and the even factors. The even factors are the ones that are divisible by two, and these factors are given below:
Even Factors of 252 = 2, 4, 6, 12, 14, 18, 28, 36, 42, 84, 126, and 252
Now, let’s move on to the odd factors of 252. All the factors that are left can be categorized as the odd factors, and these are given below:
Odd Factors of 252 = 1, 2, 7, 8, 21, and 63
Hence, we have successfully separated the even and the odd factors of 252.
Example 2
Calculate the sum of all the factors of 252 and determine if the result is a multiple of 2.
Solution
First, let’s list down all these factors. The factors of 252 are:
Factors of 252: 1, 2, 3, 4, 6, 7, 9, 12, 14, 18, 21, 28, 36, 42, 63, 84, 126, and 252
Now, let’s calculate the sum of these factors:
Sum of factors of 252 = 1 + 2 + 3 + 4 + 6 + 7 + 9 + 12 + 14 + 18 + 21 + 28 + 36 + 42 + 63 + 84 + 126 + 252
Sum of factors of 252 = 728
As the resulting number is an even number, the sum of the factors of 252 is a multiple of 2. This is evident from the multiplication process done below:
2 x 364 = 728
All images/mathematical drawings are created with GeoGebra.
