JUMP TO TOPIC
Factors of 289: Prime Factorization, Methods, Tree, and Examples
The Factors of 289 are the numbers on which 289 is completely divisible, meaning that these numbers leave zero as a remainder when 289 is divided from them. Not only do these numbers yield zero as the remainder, but they also produce a whole number quotient.
Figure 1 – All factors of 289
What are the Factors of 289?
The factors of 289 are 1, 17, and 289. So, in total, the number 289 has three factors. When 289 is divided by these factors, a whole number quotient is obtained. These factors of 289 can be grouped into factor pairs as well. The number 289 is an odd composite number and is also the perfect square of the number 17.How to Calculate the Factors of 289?
You can calculate the factors of 289 by various methods but the two most popular methods are the division method and the prime factorization method.These methods are used to determine the factors of 289. Let’s take a look at the division method first. The rule of the division method is that at the end of the division, the remainder should always be zero,Another rule for the division method is that a whole number quotient must be obtained at the end of the division. Keeping these rules in mind, let’s determine the factors of 289 by the division method.\[ \frac{289}{1} = 289 \]\[ \frac{289}{2} = 144.5 \]Since a whole number quotient is not obtained from the division of 289 by 2, so 2 is not a factor. Also, as 289 is an odd number, so al the multiples of 2 cannot act as factors of 289.Let’s try another number:\[ \frac{289}{3} = 96.33 \]This indicates that the number 3 is also not a factor.As mentioned above, the number 289 is a special odd composite number which is also the perfect square of 17. So let’s take a look at the following division:\[ \frac{289}{17} = 17 \]Hence, the number 17 is a factor of 289. Lastly, let’s consider the number itself:\[ \frac{289}{289} =1 \]Hence, the number 289 has three factors and these three factors are given below:Factors of 289 = 1, 17, 289
Factors of 289 by Prime Factorization
Prime Factorization is the method for determining the prime factors of the number. Prime factorization is also a type of division in which the division process continues till 1 is received at the end of the division process.In prime factorization, the division is carried out with the help of prime numbers.In our case of the number 289, we know that 2 cannot be used in the prime factorization as the number is odd. We have also determined that a whole number quotient is not obtained when 289 is divided by the prime number 3.So the only prime number 289 that can be divided in order to obtain prime factors is the number 17. This division is also shown below:\[ \frac{289}{17} = 17 \]Hence, the prime factorization of the number 289 is shown below: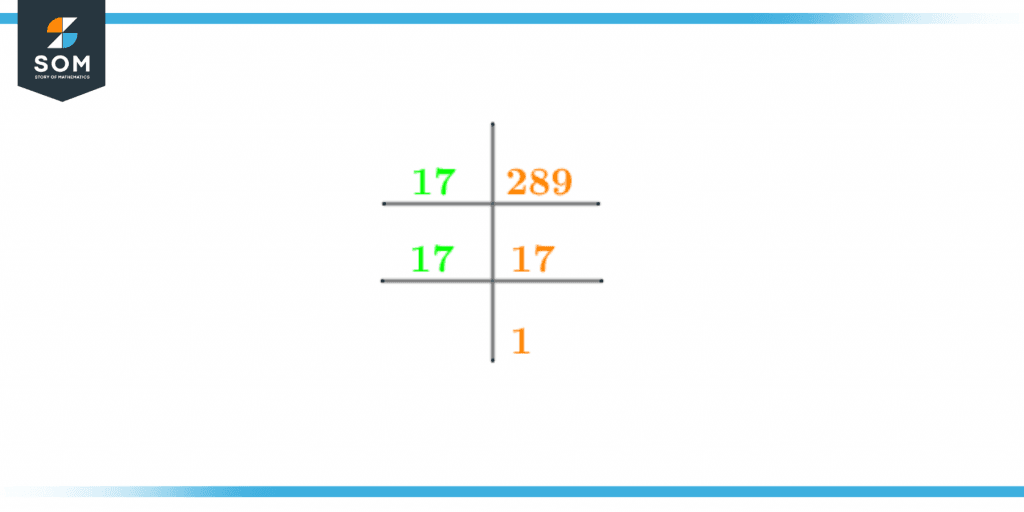
Figure 2 – Prime factorization of 289
Prime Factorization of 289 = 17 x 17
Prime Factorization of 289 = $17^{2}$
Factor Tree of 289
A Factor Tree is a visual representation of the prime factorization or the division of the number to obtain its factors. The factor tree starts with the number itself and extends out its branches into a prime number and a whole number quotient. These branches keep on extending until prime numbers are obtained at the end of the factor tree.According to the prime factorization of 289, since the prime number yielded at the end of the division of 289 is 17, the factor tree must have 17 at its end branches.The factor tree for the number 289 is shown below: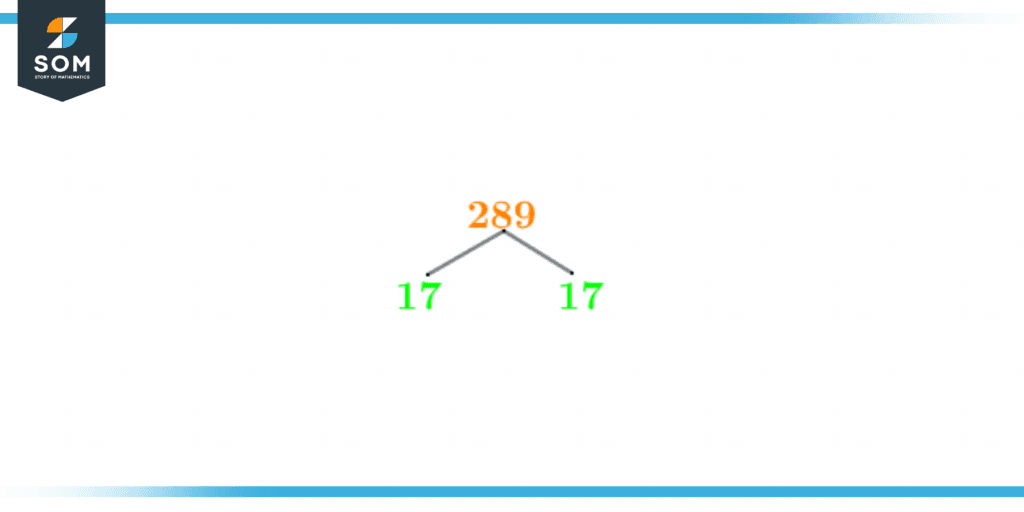
Figure 3 – Factor tree of 289
Factors of 289 in Pairs
An interesting fact about the factors of a number is that these factors can be grouped into factor pairs. These numbers which are grouped in a pair produce the original number when they are multiplied together.In this case, the number is 289. So the factor pairs of 289 will be all the possible factors that produce 289 when multiplied together.The factors of 289 are given below:Factors of 289 = 1, 17, 289
These factors can be grouped into the following pairs:1 x 289 = 289
17 x 17 = 289
Hence the factor pairs of 289 are given below:Factor Pairs of 289 = (1, 289), (17, 17)
Note that these factor pairs can be negative as well since the product that’s generated from multiplying negative numbers is a positive number.Hence, the negative factor pairs are given below:Factor Pairs of 289 = (-1, -289), (-17, -17)
Factors of 289 Solved Example
To further clarify the concept regarding the factors of 289, consider the solved example given below.Example 1
Calculate the average of the smallest and the largest factor of 289.Solution
To determine this average, let’s first take a look at the factors of 289:Factors of 289 = 1, 17, 289 Since the smallest factor of 289 is 1 and the largest factor is 289 itself, so we will be calculating the average of these two numbers.\[ Average = \frac{1+289}{2} \]\[ Average = \frac{290}{2} \]Average = 145
Hence, the average of the smallest and the largest factors of 289 is 145.