JUMP TO TOPIC
Factors of 294: Prime Factorization, Methods, and Examples
The factors of 294 are natural numbers that can divide 294 evenly. Other factors can also be described as the numbers that are completely divisible by 294.

It is an even number and also a composite which means that it has more than two factors.
Factors of 294
Here are the factors of number 294.
Factors of 294: 1, 2, 3, 6, 7, 14, 21, 42, 49, 98, 147, and 294
Negative Factors of 294
The negative factors of 294 are similar to their positive aspects, just with a negative sign.
Negative Factors of 294: -1, -2, -3, -6, -7, -14, -21, -42, -49, -98, -147, and -294
Prime Factorization of 294
The prime factorization of 294 is the way of expressing its prime factors in the product form.
Prime Factorization: 2 x 3 x 7 x 7
In this article, we will learn about the factors of 294 and how to find them using various techniques such as upside-down division, prime factorization, and factor tree.
What Are the Factors of 294?
The factors of 294 are 1, 2, 3, 6, 7, 14, 21, 42, 49, 98, 147, and 294. These numbers are the factors as they do not leave any remainder when divided by 294.
The factors of 294 are classified as prime numbers and composite numbers. The prime factors of the number 294 can be determined using the prime factorization technique.
How To Find the Factors of 294?
You can find the factors of 294 by using the rules of divisibility. The divisibility rule states that any number, when divided by any other natural number, is said to be divisible by the number if the quotient is the whole number and the resulting remainder is zero.
To find the factors of 294, create a list containing the numbers that are exactly divisible by 294 with zero remainders. One important thing to note is that 1 and 294 are the 294’s factors as every natural number has 1 and the number itself as its factor.
1 is also called the universal factor of every number. The factors of 294 are determined as follows:
\[\dfrac{294}{1} = 294\]
\[\dfrac{294}{2} = 147\]
\[\dfrac{294}{3} = 98\]
\[\dfrac{294}{6} = 49\]
\[\dfrac{294}{7} = 42\]
\[\dfrac{294}{14} = 21\]
\[\dfrac{294}{294} = 1\]
Therefore, 1, 2, 3, 6, 7, 14, 21, 42, 49, 98, 147, and 294 are the factors of 294.
Total Number of Factors of 294
For 294, there are twelve positive factors and twelve negative ones. So in total, there are twenty-four factors of 294.
To find the total number of factors of the given number, follow the procedure mentioned below:
- Find the factorization/prime factorization of the given number.
- Demonstrate the prime factorization of the number in the form of exponent form.
- Add 1 to each of the exponents of the prime factor.
- Now, multiply the resulting exponents together. This obtained product is equivalent to the total number of factors of the given number.
By following this procedure, the total number of factors of 294 is given as:
Factorization of 294 is 1 x 2 x 3 x 7$^2$.
The exponent of 1, 2, and 3 is 1. The exponent of 7 is 2.
Adding 1 to each and multiplying them together results in 24.
Therefore, the total number of factors of 294 is 24. Twelve factors are positive, and twelve factors are negative.
Important Notes
Here are some essential points that must be considered while finding the factors of any given number:
- The factor of any given number must be a whole number.
- The factors of the number cannot be in the form of decimals or fractions.
- Factors can be positive as well as negative.
- Negative factors are the additive inverse of the positive factors of a given number.
- The factor of a number cannot be greater than that number.
- Every even number has 2 as its prime factor, the smallest prime factor.
Factors of 294 by Prime Factorization
The number 294 is a composite. Prime factorization is a valuable technique for finding the number’s prime factors and expressing the number as the product of its prime factors.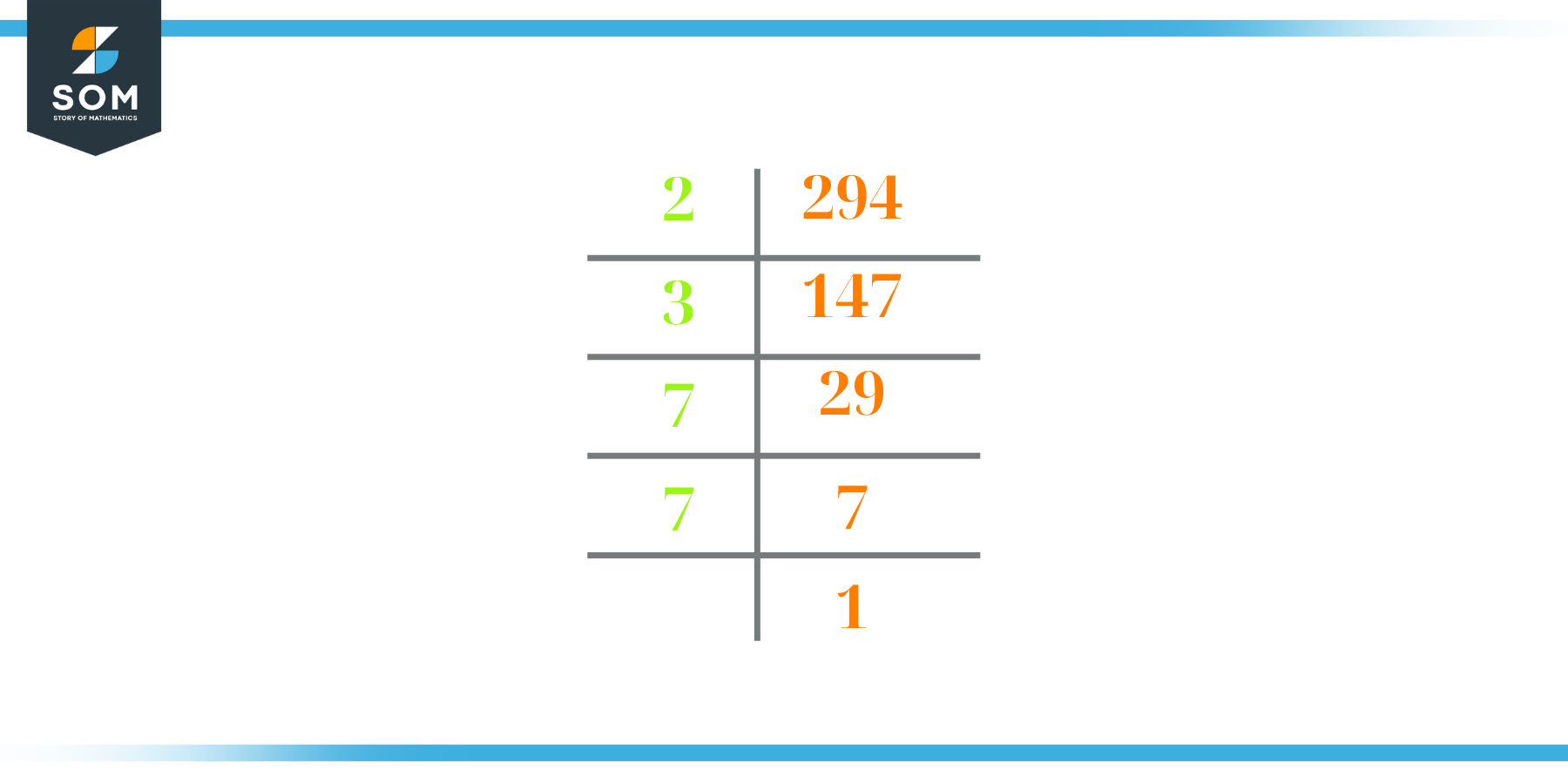
Before finding the factors of 294 using prime factorization, let us find out what prime factors are. Prime factors are the factors of any given number that are only divisible by 1 and themselves.
To start the prime factorization of 294, start dividing by its most minor prime factor. First, determine that the given number is either even or odd. If it is an even number, then 2 will be the smallest prime factor.
Continue splitting the quotient obtained until 1 is received as the quotient. The prime factorization of 294 can be expressed as:
294 = 2 x 3 x 7 x 7
Factors of 294 in Pairs
The factor pairs are the duplet of numbers that, when multiplied together, result in the factorized number. Factor pairs can be more than one depending on the total number of factors given.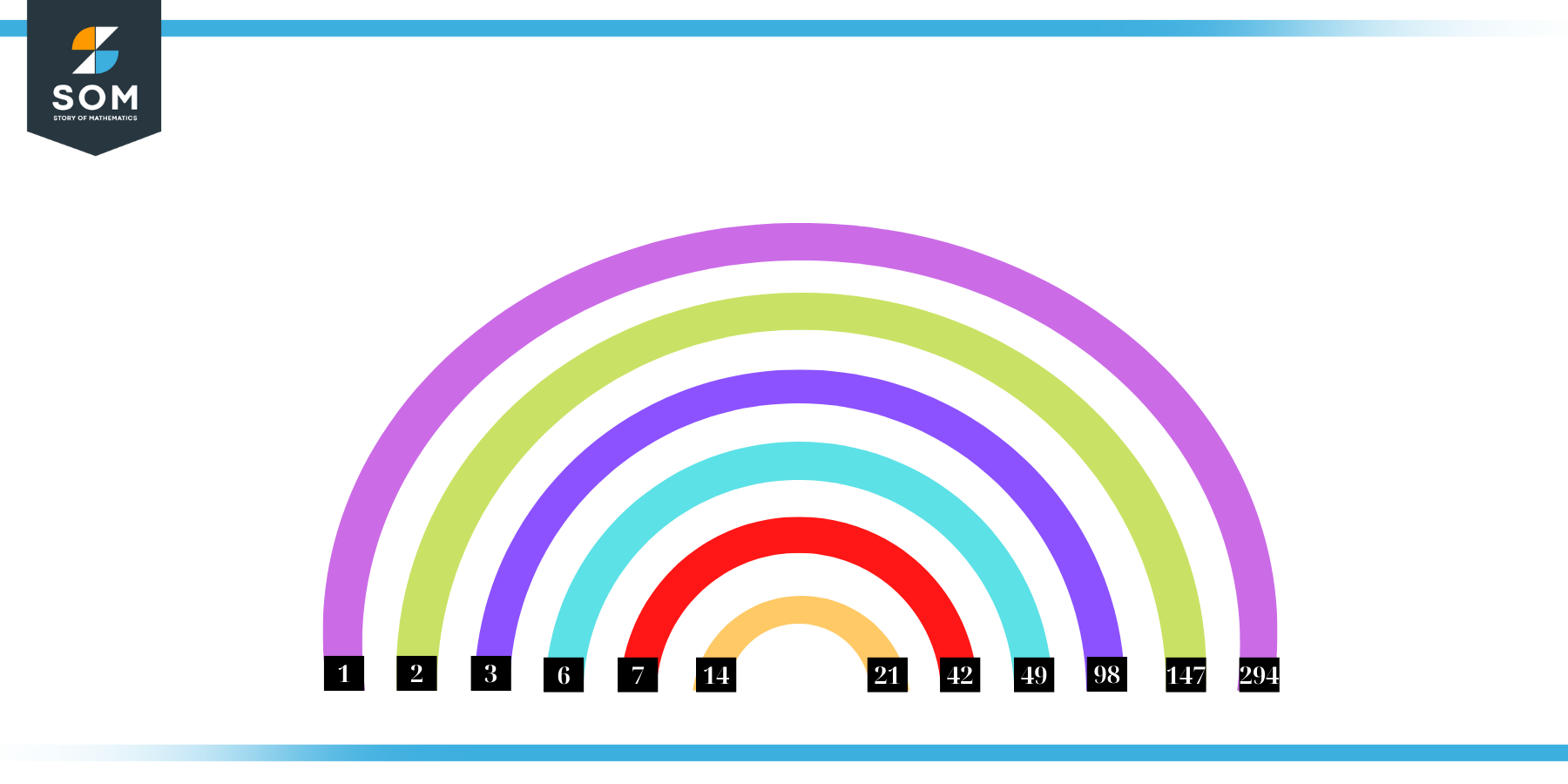
For 294, the factor pairs can be found as:
1 x 294 = 294
2 x 147 = 294
3 x 98 = 294
6 x 49 = 294
7 x 42 = 294
14 x 21 = 294
The possible factor pairs of 294 are given as (1, 294), (2, 147), (3, 98), (6, 47), (7, 42), and (14, 21).
All these numbers in pairs, when multiplied, give 294 as the product.
The negative factor pairs of 294 are given as:
-1 x -294 = 294
-2 x -147 = 294
-3 x -98 = 294
-6 x -49 = 294
-7 x -42 = 294
-14 x -21 = 294
It is important to note that in negative factor pairs, the minus sign has been multiplied by the minus sign, due to which the resulting product is the original positive number. Therefore, -1, -2, -3, -6, -7, -14, -21, -42, -49, -98, -147, and -294 are called negative factors of 294.
Factors of 294 Solved Examples
To better understand the concept of factors, let’s solve some examples.
Example 1
How many factors of 294 are there?
Solution
The total number of Factors of 294 is twelve.
Factors of 294 are 1, 2, 3, 6, 7, 14, 21, 42, 49, 98, 147, and 294.
Example 2
Find the factors of 294 using prime factorization.
Solution
The prime factorization of 294 is given as:
294 $\div$ 2 = 147
147 $\div$ 3 = 69
69 $\div$ 7 = 7
7 $\div$ 7 = 1
So the prime factorization of 294 can be written as:
2 x 3 x 7 x 7 = 294
