JUMP TO TOPIC
Factors of 32: Prime Factorization, Methods, and Examples
All the numbers that completely and perfectly divide the number 32, give a whole number in the quotient, and leave zero as the remainder are called the factors of 32.

Figure 1 – All possible Factors of 32
Factors of 32 can also be referred to as the pair of two numbers that multiply to give the number 32 as the product.
This article comprehends the details of the factors of 32 and how to find these factors by using different methods which fundamentally are prime factorization and division methods.
What Are the Factors of 32?
The factors of 32 are 1, 2, 4, 8, 16, and 32.
Since 32 is an even composite number, it has 6 factors which are stated above. All the mentioned numbers are divisors of 32 because when the number 32 is subjected to divide by any of the said numbers, it is divided completely and leaves zero or nothing as a remainder.
How to Calculate the Factors of 32?
You can find the factors of number 32 by using the division method. For this purpose, start dividing 32 by the smallest natural number that divides 32 perfectly without leaving any remainder behind.
Divide 32 by the smallest natural number which is 1.
\[\dfrac{32}{1} = 32 \]
As 1 has completely divided 32 without leaving any remainder. So, 1 is a factor of 32.
Now divide 32 by the smallest even prime number which is 2.
\[\dfrac{32}{2} = 16 \]
As the number 32 has been divided evenly by its divisor. So, 2 is also a factor of 32.
To achieve more factors, divided 32 by natural numbers that completely divide 32 and leave zero remainders as shown below:
\[\dfrac{32}{4} = 8 \]
\[\dfrac{32}{8} = 4 \]
\[\dfrac{32}{16} = 2 \]
\[\dfrac{32}{32} = 1\]
It is clear that the number 32 has completely been divided by these numbers and has left no remainder. Therefore, all the numbers 1, 2, 4, 8, 16, and 32 are factors of 32.
Properties of the number 32
Here are the properties of the number 32 which must be kept in mind to find out factors of 32.
- 32 is an even number.
- 32 is a composite number.
- 32 is not a perfect square.
- The Cross sum of 32 is 5.
Important Facts About Factors of 32
- The number 1 is the smallest factor of 32.
- The number 32 cannot have any factor which is larger than itself. Hence 32 is the largest factor of the number 32.
- Except for 1, all the factors of 32 are even factors.
- 32 has only one prime factor. Please note that 1 is not a prime number.
- The number 32 has 4 composite factors.
- 32 has only one odd factor which is 1.
- The Sum of divisors of 32 is 63.
Factors of 32 by Prime Factorization
The representation of the number 32 as a product of all of its prime factors is termed the prime factorization of the number 32. Prime factorization, being one of the principal methods, can be used to find out the factors of 32.
To achieve the purpose, divide 32 by the smallest prime number which divides 32 perfectly without leaving any remainder. The quotient resulting from the division is divided again by the smallest prime number and the procedure goes on until 1 is left as the final quotient which cannot be divided anymore.
Following are the steps to calculate factors of 32 by the prime factorization method.
The first step in the procedure is to divide 32 by the smallest possible prime number which is 2 in this case.
\[\dfrac{32}{2} = 16 \]
As the quotient 16 is an even composite number, it can further be divided by 2 which is the smallest available prime number.
\[\dfrac{16}{2} = 8 \]
The number 8, again, is even composite and requires to be further divided by the prime number 2.
\[\dfrac{8}{2} = 4 \]
The quotient 4 now can be further divided by 2 and thus give the next quotient as 1
\[\dfrac{4}{2} = 1 \]
The quotient 1 cannot be divided any further.
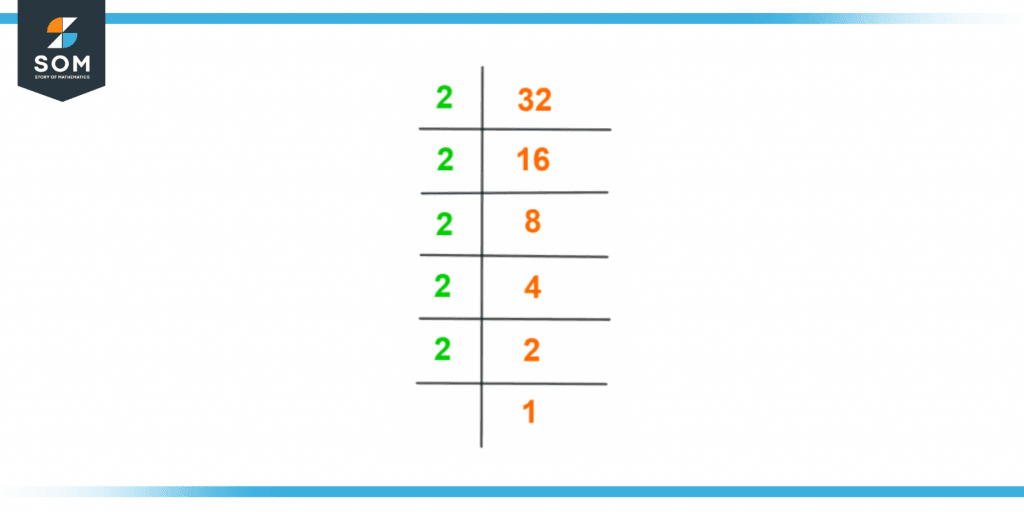
Figure 2 – Prime Factorization of 32
Therefore, the prime factorization of 32 can be expressed as follows:
32 = 2 x 2 x 2 x 2 x 2
It can also be expressed as:
\[ 32 = 2^5 \]
Factor Tree of 32
A factor tree is another method to express the factors of 32 where the prime factorization of the number 32 is illustrated in the form of a tree whose branches depict the divisors of the given number.
The splitting of a branch can result in the production of either a prime or composite number. If any one of the two branches resulting from a split produces a composite number, the branching keeps going down until a split produces prime numbers on both of its branches. This is where the branching stops.
If we write 32 into multiples, it would be: 32 = 2 x 16
Upon dividing 16 into its multiples, it would be: 16 = 2 x 8
Dividing 8 further into its multiples would result in 8 = 2 x 4
Further dividing 4 into its multiple factors would give: 4 = 2 x 2
By dividing 2 further into its multiples, it would be: 2 = 2 x 1
Expressing the number in terms of prime factors would be as follows:
2 x 2 x 2 x 2 x 2
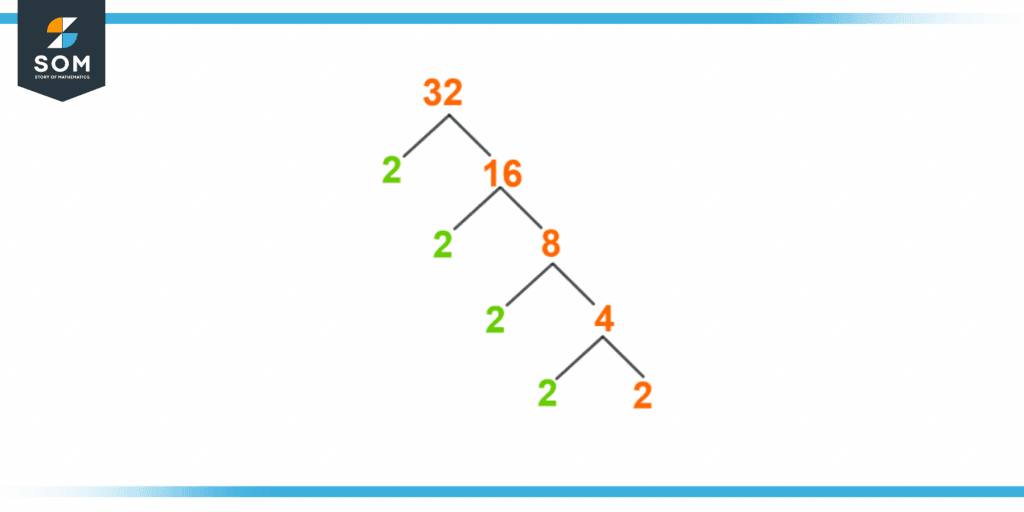
Figure 3 – Factor Tree of 32
Factors of 32 in Pairs
A set of two natural numbers, which multiply to give the number 32 are called factors of 32 in pairs i.e. the product of the factors of a number represented in the form of pairs.
1 x 32 = 32
2 x 16 = 32
4 x 8 = 32
8 x 4 = 32
16 x 2 = 32
The number 32 has 6 factors in total which can be written in pairs as follows:
(1, 32)
(2, 16)
(4, 8)
(8, 4)
(2, 16)
(1, 32)
As the multiplication of two negative factors also produces a positive product, the number 32 can have negative pair factors as well.
(-1) x (-32) = 32
(-2) x (-16) = 32
(-4) x (-8) = 32
Here are the negative pair factors of number 32:
(-1, -32)
(-2, -16)
(-4, -8)
Important Tips
- A given number can only have integers and whole numbers as its factors.
- Factors/divisors of a given number cannot be in decimals or fractions.
- All the positive pair factors of a number are also pair factors of the same number in their negative form.
Factors of 32 Solved Examples
Example 1
Sophia has been given sets of pair factors of 32. She has been asked to pick the following:
- A pair factor with one prime and one composite number.
- A pair factor with one odd and one even number.
Please help her to pick the above-asked pair factors from the four given sets of pair factors.
(2, 16)
(4, 8)
(1, 32)
(6, 12)
Solution
In the given sets of pair factors, first sort out the sets which contain prime and odd factors. As we know from the numbers mentioned in the above sets, only 2 is a prime number and 1 is the only odd number.
Hence, the factor pair consisting of one prime number and one composite number is:
(2, 16)
And the factor pair containing one odd and an even number is
(1, 32)
Example 2
A class teacher brought a pack of chocolates to her class of 40 students. She distributed 4 chocolates each among 8 students who achieved A+ grades. Please calculate the total how many chocolates were districted among students.
Solution
The number of chocolates distributed among students can be found by the product of the number of students and the number of chocolates each student got.
Number of students = 8
Number of chocolates distributed = 4
Total number of chocolates distributed = 8 x 4
Total number of chocolates distributed = 32
Hence, a total of 32 chocolates were distributed among 8 students.
Example 3
Name the methods by which factors of 32 can be found.
Solution
Factors of 32 can be found by following methods:
- Division Method
- Multiplication Method.
- Prime Factorization Method.
- Factor Tree Method.
Example 4
Which of the following statement is False about factors of 32?
- 32 has a total of 6 factors.
- 32 has only one prime factor which is 2.
- 32 can have one positive and one negative factor in the pair.
- Pair Factors of 32 can have one prime and one composite number.
Solution
The product of one positive and one negative number is always negative. Hence, 32 can never have one positive and another negative factor in pairs. So the False statement is 32 can have one positive and one negative factor in pairs.
Images/mathematical drawings are created with GeoGebra.
