JUMP TO TOPIC
Factors of 336: Prime Factorization, Methods, Tree, and Examples
Factors of 336 are those numbers when divide or multiplied give either whole numbers or the number 336 itself. It can be further defined as the product of any two numbers multiplied together to give the number 336. This method is called the multiplication method.
Figure 1 – All factors of 336
What Are the Factors of 336?
The factors of 336 are listed as 1, 2, 3, 4, 6, 7, 8, 12, 14, 16, 21, 24, 28, 42, 48, 56, 84, 112, 168, and 336. When 336 is divided by any number to give a whole number then it is known as a factor.336 is an even composite number which means that it has more than the typical two factors which every number has such as 1 and the number itself.How To Calculate the Factors of 336?
You can calculate the factors of 336 by determining the numbers that can divide 336 evenly without any remainder. The list of the number completely dividing 336 is given as:\[ \dfrac{336}{1}=336\]remainder = 0
\[ \dfrac{336}{2}=168\]remainder = 0
\[ \dfrac{336}{3}=112\] remainder = 0
\[ \dfrac{336}{4}=84\] remainder = 0
\[ \dfrac{336}{6}=56\] remainder = 0
\[ \dfrac{336}{7}=48\] remainder = 0
\[ \dfrac{336}{8}=42\] remainder = 0
\[ \dfrac{336}{12}=28\]remainder = 0
\[ \dfrac{336}{14}=24\] remainder = 0
\[ \dfrac{336}{16}=21\]remainder = 0
We will divide 336 by the smallest natural number i.e. 1. As we know that 1 is the factor of every possible number. So we can say that from the above calculation 1 is a factor of 336. This method is called the division method. We will repeat this process for every number which is less than 336 itself because a factor can always be less or equal to that number but it can never be greater than that number. Similarly, zero will never be considered a factor.We can also list the negative factors by following the same method in which we will divide a negative integer by 336 and if the answer gives zero remainders and is a whole number then it will be a factor too.So we can summarize the factor list of 336 as:Factors of 336 = 1, 2, 3, 4, 6, 7, 8, 12, 14, 16, 21, 24, 28, 42, 48, 56, 84, 112, 168, 336 For the negative factors, we can list the factors as:Negative Factors of 336 = -1, -2, -3, -4, -6, -7, -8, -12, -14, -16, -21, -24, -28, -42, -48, -56, -84, -112, -168, -336 We can also find factors through an alternative method which is the multiplication method for finding the factors. So we will calculate the factors of 336 by multiplying any two numbers and if the product of those numbers is equal to 336 then we will consider those numbers as the factors of 336. Given below is the method to find the factors of 336 by the multiplication method.1 x 336 = 336
This method is also called the Factor Pairing method.Factors of 336 by Prime Factorization
The result of the product of prime numbers can be written as Prime Factorization of the product. As 336 is a composite number so we can do its prime factorization by following these steps:\[ \dfrac{336}{2}=168\]\[ \dfrac{168}{2}=84\]\[ \dfrac{84}{2}=42\]\[ \dfrac{42}{2}=21\]\[ \dfrac{21}{3}=7\]\[ \dfrac{7}{7}=1\]For Prime factorization, we will take the smallest prime factor i.e 2. We will divide 336 by 2. The answer will also be a factor of 336. We will divide the answer by 2. We will keep on doing this method until we get a decimal number. If so we will shift to another prime factor of 336 and we will keep on repeating this method till we get 1 in the answer. So Prime factorization of 336 can be written as:2 x 2 x 2 x 2 x 3 x 7 = 336
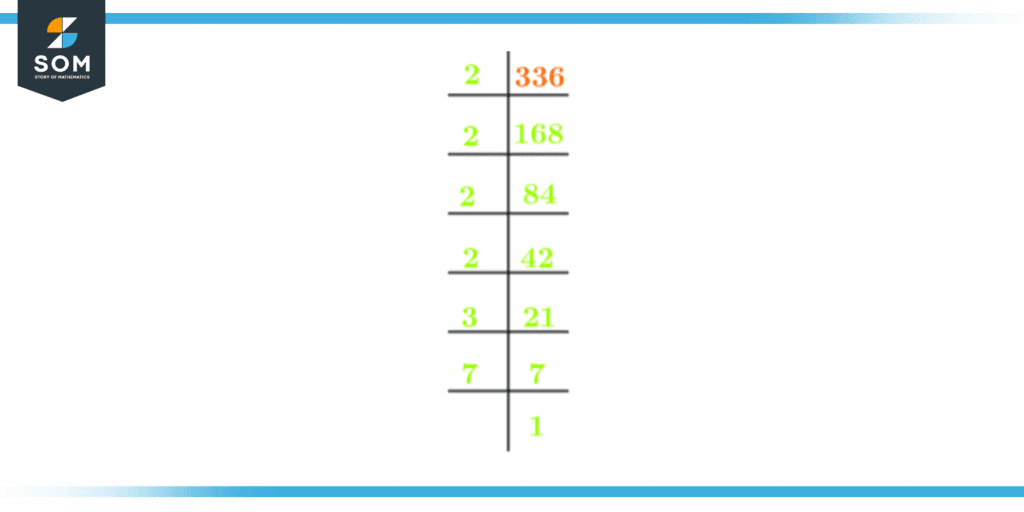
Figure 2 – Prime factorization of 336
Factor Tree of 336
We use a factor tree to demonstrate all of the prime factors of a number except for 1 because it is not a prime number. We use a graphical display to understand the concepts of the factor tree. In total, 336 have 6 Prime Factors. 2 is raised to the power of 4 along with 3 and 7.The diagram given below is called a factor tree of 336.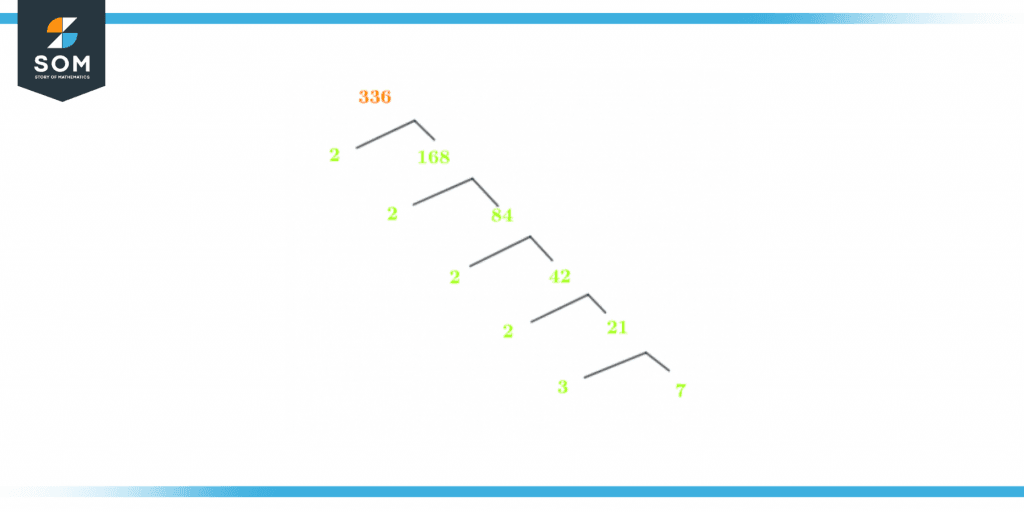
Factor tree of 336
Factors of 336 in Pairs
When two specific numbers are multiplied with each other and the product is equal to 336 then we can say that those two numbers are the Factor Pair of 336. So by definition factor pair is the product of any two numbers that gives the desired number. For 336 we will find factor pairs in this way:1 x 336 = 336
2 x 168 = 336
3 x 112 = 336
4 x 84 = 336
6 x 56 = 336
7 x 48 = 336
8 x 42 = 336
12 x 28 = 336
14 x 24 = 336
16 x 21 = 336
We can use the same method to find the negative factors of 336. As we know that when 2 minus signs are multiplied they cancel off each other’s effect so we will get the positive number in the answer.Now for the negative factors of 336, we can also find the factor pairs.-1 x -336 = 336
-2 x -168 = 336
-3 x -112 = 336
-4 x -84 = 336
-6 x -56 = 336
-7 x -48 = 336
-8 x -42 = 336
-12 x -28 = 336
-14 x -24 = 336
-16 x -21 = 336
So we can write the pairs in this way as given below.(1, 336)
(2, 168)
(3, 112)
(4, 84)
(6, 56)
(7, 48)
(8, 42)
(12, 28)
(14, 24)
(16, 21)
Negative Factor Pair of 336 are given as:(-1, -336)
(-2, -168)
(-3, -112)
(-4, -84)
(-6, -56)
(-7, -48)
(-8, -42)
(-12, -28)
(-14, -24)
(-16, -21)
