JUMP TO TOPIC
Factors of 35: Prime Factorization, Methods, Tree, and Examples
Factors of 35 are the numbers that evenly divide 35 without leaving any remainder. Factors are always in the form of whole numbers.
Figure 1 – All possible Factors of 35
- Positive Factors
- Negative Factors
What Are the Factors of 35?
Factors of 35 are 1, 5, 7, and 35; all of these numbers divide 35 evenly. The remainder is zero.35 is an odd composite number. A number having more than two factors is known as the composite number. There are eight total factors of 35. Four are positive factors and the other four are negative factors.How To Calculate the Factors of 35?
You can calculate the factors of 35 by two methods: division and multiplication method. We will discuss both ways in this article.As the number 35 is composite, there are more than two factors of 35. Make a number line starting from 1 and ending on 35. We have to find the factors in between them.Factors of 35 by division method:One is a factor of every whole number because every number is completely divided by 1.\[ \frac{35}{1} = 35 \]\[ \frac{35}{-1} = -35 \]1 and -1 are factors of 35.35 is not even, so it wouldn’t be divided by 2.Let’s divide 35 by 3:\[ \frac{35}{3} = 11.66 \]When we divide 35 by 3, the number is not evenly divided. The remainder is 2. Condition of factors is not satisfied 3 is not a factor of 35. Divide 35 by 5:\[ \frac{35}{5} = 7 \]\[ \frac{35}{-5} = -7 \]When 35 is divided by 5. The number is not evenly divided. The remainder is 0. Condition of factors is satisfied 5 and -5 are the factors of 35.Divide 35 by 6:\[ \frac{35}{6} = 5.83 \]When we divide 35 by 5, the condition of factors is not satisfied. The remainder is 5. As a result of the above calculation 6 is not a factor of 35. Divide 35 by 7:\[ \frac{35}{7} = 5 \]\[ \frac{35}{-7} = -5 \]When 35 is divided by 7. The remainder is 0. Condition of factors is satisfied 7 and -7 are the factors of 35.Divide 35 by 11:\[ \frac{35}{11} = 3.18 \]When 35 is divided by 11. Condition of factors is not satisfied. The remainder is 2. As a result of the above calculation 11 is not a factor of 35.Every number is a factor in itself. As every number divides itself evenly and the remainder is always zero. 35 and -35 are the factors of 35.Positive factors of 35 = 1, 5, 7, 35. Negative factors of 35 = -1, -5, -7, -35. Factors of 35 by multiplication method:1 x 35 = 35
-1 x -35 = 35
When a negative sign is multiplied by a negative sign, the product is always positive.By the above multiplication, we conclude that 1, -1, 35, and -35 both are factors of 355 x 7 = 35
-5 x -7 = 35
Factors of 35 are 1, -1, 5, -5, 35, and -35.Factors of 35 by Prime Factorization
The technique used to write the number 35 as the product of its prime factors is known as Prime Factorization. Prime factorization is a mathematical process in which we discover the prime factors of a number, and we obtain the original number when multiplied together. This method is only applicable to composite numbers. The two most common ways of finding prime factorizations are the following:- Division method.
- Factor tree.
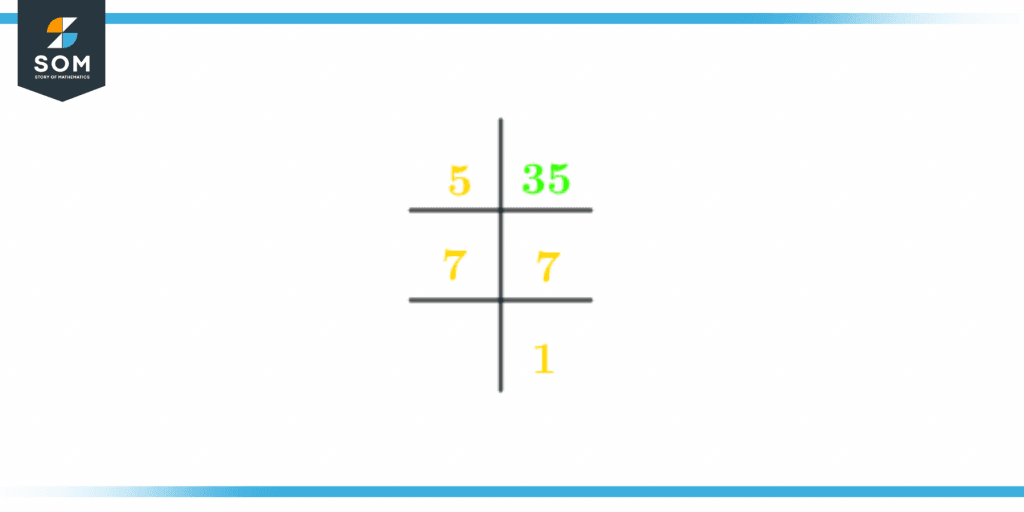
Figure 2 – Prime Factorization of 35
Factor Tree of 35
The factor tree is a pictorial representation of factors of a number, specifically the prime factors. A factor tree is just like a tree that has many branches. Every branch further splits with some logic.Now we will learn how to construct a factor tree:Write the number at the top. Draw two branches out of it. Fill these branches with the factors of the number. Keep on dividing until each branch ends up with the prime factors.The factor tree of 35 is shown below in figure 2: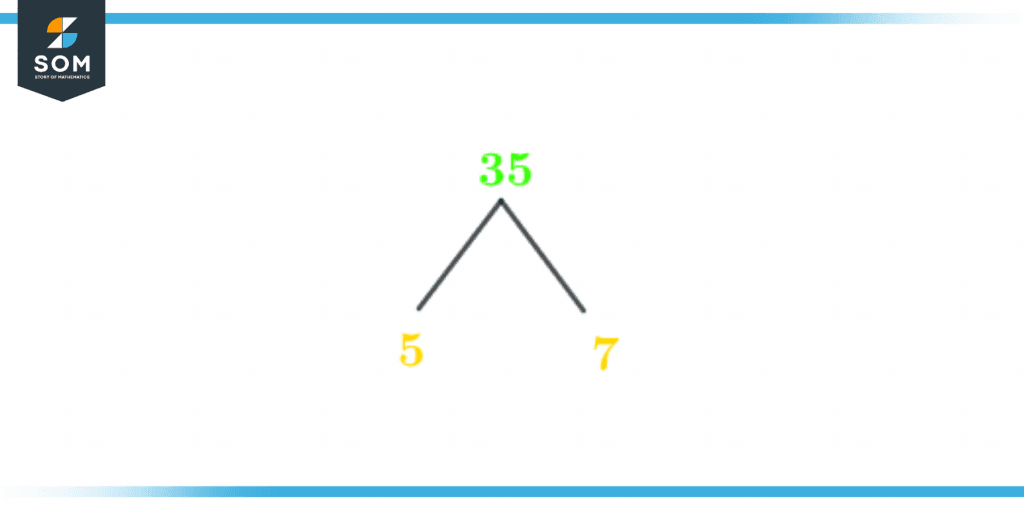
Figure 3 – Factor Tree of 35
Prime Factorization of 35 : 5 x 7
Factors of 35 in Pairs
Writing a set of two factors of 35. When multiplied gives a particular answer, which is equal to the original number. Factor pairs of a number can be calculated by the simple multiplication method. Factor pairs can be positive and negative, but they can’t be in fractional form.Finding factor pairs using the multiplication method:1 x 35 = 35
5 x 7 = 35
The positive factor pairs of 35 are the following:(1, 35)
(5, 7)
Finding negative factors of 35:-1 x -35 = 35
-5 x -7 = 35
The negative factor pairs of 35 are the following:(-1, -35)
(-5, -7)
Factors of 35 Solved Examples
Following are some solved examples for a better understanding regarding factors of 35.Example 1
Rachel has 35 red boxes and Maya has 75 green boxes. They want to arrange the boxes in such a way that each row contains an equal number of boxes and also each row should have only red boxes or green boxes. What is the greatest number of boxes that can be arranged in each row?Solution
The given condition is:The number of boxes should be equal in each row.Each row should have a single color of boxes.To arrange the green and red boxes in an equal number of rows find the largest common factor between 35 and 75.Firstly, find the factors of numbers 35 and 75 are as follows:Factors of 35 = 1, 5, 7, 35 Factors of 75 = 1, 3, 5, 15, 25, 75From the list of factors of 35 and 75. Now find the HCF (Highest Common Factor).GCF of 35 and 75 = 5 5 is also a common factor of 35 and 75.Each row will have 5 boxes Rows of red boxes: \[ \frac{35}{5} = 7 \]Rows of red boxes: \[ \frac{75}{5} = 15 \]Example 2
Find the sum of all factors of 35 and divide it by the sum of even factors of 35.Solution
Factors of 35 = 1, 5, 7, 35.Finding the sum of all factors of 35Sum: 1 + 5 + 7 + 35 = 48
35 is an odd number, and factors of 35 are also odd. \[ \frac{48}{1} = 48 \]