JUMP TO TOPIC
Factors of 42: Prime Factorization, Methods, Tree, and Examples
Factors are numbers or mathematical expressions, that when undergoing division, divide the number completely, without leaving any remainder behind. In other words, factors of a given number are also referred to as their divisors.
Figure 1 – All possible Factors of 42
What Are the Factors of 42?
The factors 42 are 1, 2, 3, 6, 7, 14, 21, and 42. All the above-mentioned numbers are recognized as factors of the number 42 as these are the set of integers that when divided by the number 42, result in producing zero as the remainder. The number 42 has factors besides just itself and the number 1 since it is an even and composite number. In simple words, the total number of factors of number 42 is 8, as stated above.How To Calculate the Factors of 42?
You can calculate the factors of 42 simply by using the universally used multiplication or division methods as one of the primary techniques. In this article, we are going to use both techniques to find the required factors of the number 42. Initially, we are going to multiply different pairs of integers to get the desired product, of 42. Such that, the set of numbers that produce 42 as their result will be termed as the proposed factors of the number 42. The following is the list of pair-multiplication for the number 42,1 x 42 = 42
Similarly,2 x 21 = 42
3 x 14 = 42
6 x 7 = 42
Hence, it has been seen that the numbers 1, 2, 3, 6, 7, 14, 21, and 42 are the factors of 42. By the previously used technique now, we are going to put light on the other most commonly celebrated approach i.e. division, to calculate the factors of 42. Here, we are going to recommend a few numbers (less than or equal to 42) and divide 42 by them in such a way that, if the division leaves no or zero remainders behind then, we are going to refer to the old suggested number as the factor of 42. Now, let’s start the division of 42 by the different sets of integers. The following steps are to be adopted to calculate the factors of 42.At first, divide 42 by the smallest recommended number i.e. 1. Check for the remainder. Is the remainder zero?\[ \dfrac {42}{1} = 42, r=0 \]Yes, the remainder is zero. Hence, it is proved that the number 1 is a factor of 42.(The number 1 is also known as the universal factor, as every number is divisible by 1) Now, divide 42 by the number 2 such that,\[ \dfrac {42}{2} = 21, r=0 \]Where the number 21 is referred to as the whole-number quotient of the above division.Additionally, as the remainder of the above division is zero, therefore, 2 is also a celebrated factor of 42.Continue using the previously mentioned procedure to divide 42 by the other set of integers.\[ \dfrac {42}{3} = 14 \]\[ \dfrac {42}{6} = 7 \] \[ \dfrac {42}{7} = 6 \]Where the numbers 14, 7, and 6 are described as the remaining whole-number quotients of the above division processes. As mentioned earlier, each number has both positive and negative factors and the negative factors of any number are the additive inverse of its positive factors. The following is the list of the negative factors of 42.Negative factors of 42 = -1, -2, -3, -6, -7, -14, -21, -42Similarly, the following is the list of the positive factors of 42.Positive factors = 1, 2, 3, 6, 7, 14, 21, 42Factors of 42 by Prime Factorization
Prime factorization is the process that focuses on dividing an integer into its prime factors until the result is 1. Integers or numbers that can only be divided equally by themselves and by one are known as prime factors. Any number that fits the conditions specified in the definition of prime factors, but never 0 or 1, can be the prime factor of a given integer because 0 and 1 are not clearly defined prime numbers. Prime factorization is a widely used technique to find the prime factors of a given number. The prime factorization of the number 42 is given as follows,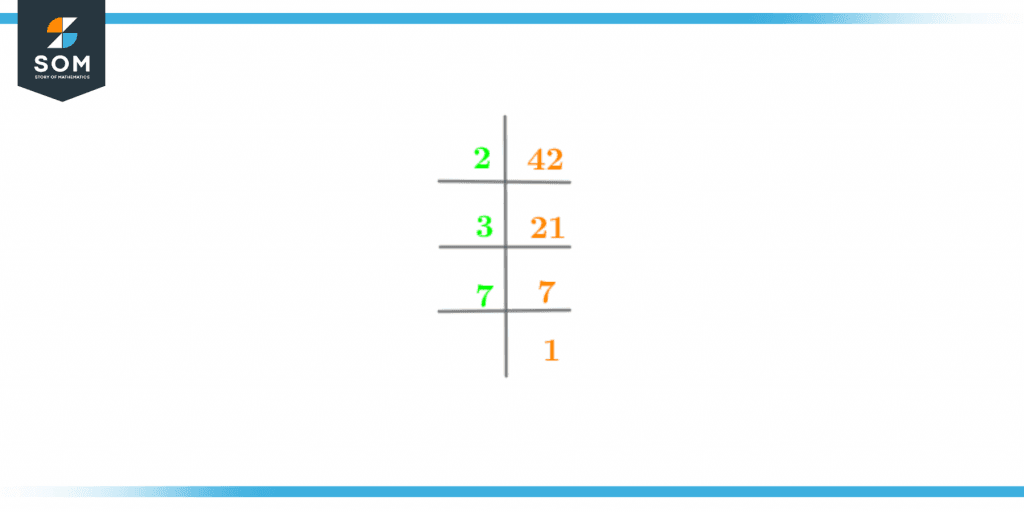
Figure 2 -Prime Factorization of 42
Also, the prime factorization of 42 can be expressed as the following expression,2 x 3 x 7 = 42
Hence, there are 3 prime factors of 42. The prime factors of 42 are: 2, 3, 7Factor Tree of 42
The geometric representation of a number’s prime factors is a factor tree.The following image shows the factor tree of the number 42,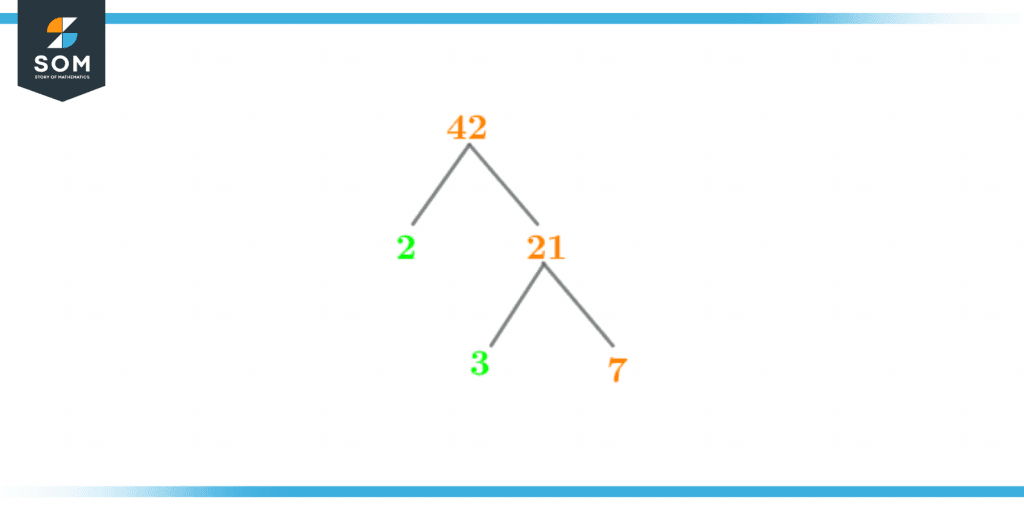
Figure 3 – Factor Tree of 42
Factors of 42 in Pairs
Factor pairs are those groups of numbers that, when multiplied together, provide the same result as the product of which they are a factor. The pair of factors can be both a set of negative or positive integers. The process used to determine the factor pair of 42 is identical to the approach used to determine the factor pairs of any other number. Consequently, the pair of factors of the number 42 are represented as,1 x 42 = 42
Where, (1, 42) is a factor pair of 42.Similarly,2 x 21 = 42
3 x 14 = 42
6 x 7 = 42
Where, (2, 21), (3, 14), and (6, 7) are the factor pairs of 42.Hence, the positive factor pairs of the number 42 are (1, 42), (2, 21), (3, 14), and (6, 7).As described earlier, the pair of factors are described in terms of both the positive and negative integers. Therefore, the negative factor pairs of 42 are (-1,-42), (-2, -21), (-3, -14), and (-6,-7).Factors of 42 Solved Examples
Now, let us solve a few examples to test our understanding of the above article.Example 1
Annie wants to calculate the average of the factors of 42. Can you help her in finding the correct answer?Solution
Given that:The factors of 42 are1, 2, 3, 6, 7, 14, 21, and 42.The average of the set of factors of 42 is achieved by calculating the sum of the above-mentioned factors, divided by the total number of factors proposed in the list.\[ Average = \frac{\text{Sum of factors}}{\text{Total number of factors}} \]Such that:\[ Average = \frac{1+2+3+6+7+14+21+42}{8} \]\[ = \frac{96}{8} \]= 12
Hence, the average of the factors of 42 is 12.