JUMP TO TOPIC
Factors of 432: Prime Factorization, Methods, Tree, and Examples
Factors of 432 are the numbers that divide 432 completely with the zero remainders. Factors are determined to express the number in terms of multiplication. The factors of numbers can be found using various mathematical techniques such as divisibility rules of numbers and the prime factorization method.

Figure 1 – All possible Factors of 432
432 has 20 factors in total. Let us find out how to find the factors of 432 and how to represent them in pairs and factor trees.
What Are the Factors of 432?
The factors of 432 are 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 27, 36, 48, 54, 72, 108, 144, 216 and 432 as all of them are entirely divisible by 432.
A number has positive as well as negative factors the only difference is that negative factors are written with a negative sign. Therefore in total, there are 40 factors of 432. It has 20 positive and 20 negative factors
How To Calculate the Factors of 432?
You can find the factors of 432 by dividing 432 by the list of integers from 1 to 432 and find which of them evenly divides 432, leaving nothing as a remainder. This is the most common method used to find the factor of a given number.
Let’s start by dividing 432 by the smallest integer which is 1.
\[ \dfrac{432}{1} = 432 \]
This shows that 1 is the factor of 432 as the remainder is zero.
Now dividing 432 by 2 since 432 is an even number it is fully divided by 2 and thus 2 is the factor of 432.
\[ \dfrac{432}{2} = 216 \]
Keep on dividing 432 by the list of numbers until all factors of 432 are determined.
The numbers that fully divide 432 and are regarded as the factors of 432 are given below:
\[ \dfrac{432}{3} = 144 \]
\[ \dfrac{432}{4} = 108 \]
\[ \dfrac{432}{6} = 72 \]
\[ \dfrac{432}{8} = 54 \]
\[ \dfrac{432}{9} = 48 \]
\[ \dfrac{432}{12} = 36 \]
\[ \dfrac{432}{16} = 27 \]
\[ \dfrac{432}{18} = 24 \]
\[ \dfrac{432}{24} = 18 \]
\[ \dfrac{432}{27} = 16 \]
\[ \dfrac{432}{36} = 12 \]
\[ \dfrac{432}{48} = 9 \]
\[ \dfrac{432}{54} = 8 \]
\[ \dfrac{432}{72} = 6 \]
\[ \dfrac{432}{108} = 4 \]
\[ \dfrac{432}{144} = 3 \]
\[ \dfrac{432}{216} = 2 \]
\[ \dfrac{432}{432} = 1 \]
So the factor list of 432 is given as:
Factor List: 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 27, 36, 48, 54, 72, 108, 144, 216 and 432.
Let’s discuss some important facts related to number 432 and its factors.
Important Facts
Here are some interesting properties of the factors of 432:
- 432 is a composite number with 20 factors.
- 432 is a unique number that has the square of its factors as well in its factors list. For instance, 2 is the factor of 432 and its square 4 is also the factor of 432.
- It is also called Achilles Number because it has the square of its prime factors as its factors.
- The sum of all the factors of 432 is 1240.
- None of the factors of 432 is in decimal form nor fractions.
Factors of 432 by Prime Factorization
Prime factorization is the easiest way to determine the prime factors of 432. It represents the number in form of its prime factors. Prime factorization can be done using the factor tree method and upside-down division.
Let’s discuss each of them individually. To start the prime factorization of 432, divide 432 by its smallest prime factor, which is 2.
\[\dfrac{432}{2} = 216 \]
The quotient 216 is received and further division is possible. Again divide 216 by 2.
\[\dfrac{216}{2} = 108 \]
108 is again an even number so divide it by 2.
\[\dfrac{108}{2} = 54 \]
Follow the same pattern and keep on dividing the obtained quotient with 2 until even numbers are obtained as quotient.
\[\dfrac{54}{2} = 27 \]
Now divide 27 by 3 and continue dividing till 1 is received.
\[\dfrac{27}{3} = 9 \]
\[\dfrac{9}{3} = 3 \]
\[\dfrac{3}{3} = 1 \]
So, the prime factorization of 432 is given as:
432 = 2 x 2 x 2 x 2 x 3 x 3 x 3
The prime factorization of 432 in the upside-down division is shown in figure 1 below:
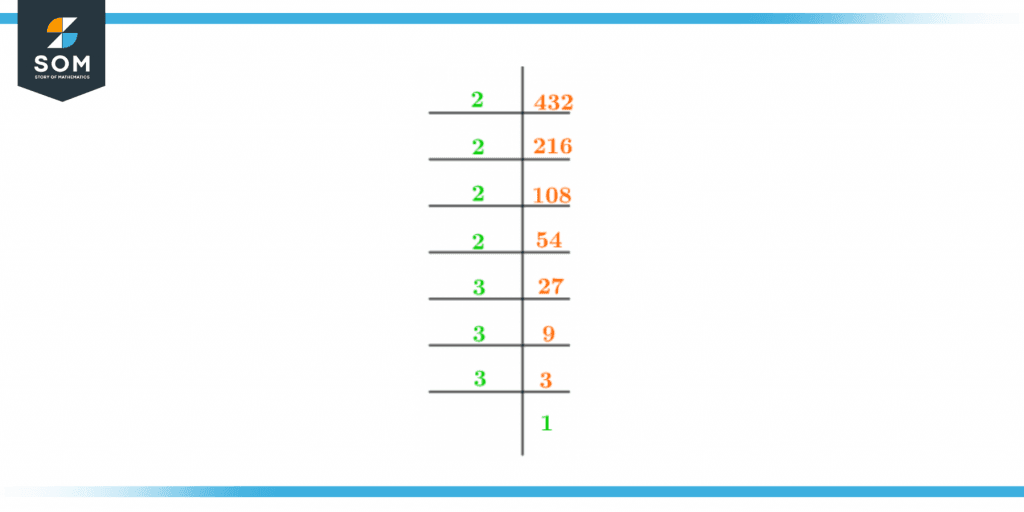
Figure 2 – Prime Factorization of 432
Factor Tree of 432
Factor tree of 432 is its prime factors representation in the form of a tree diagram. The factor tree of 432 is shown in figure 2 below:
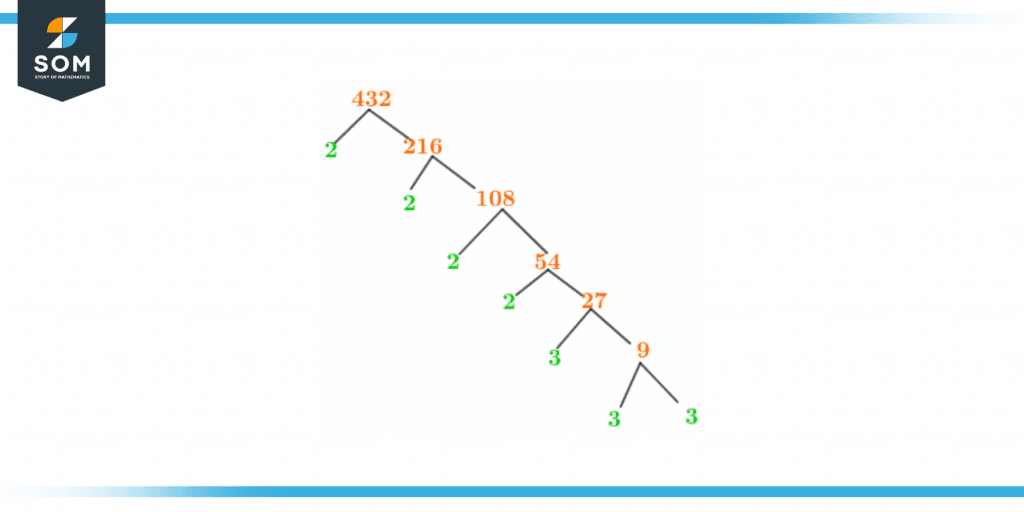
Figure 3 – Factor Tree of 432
The factors of any given number in the form of pairs that when multiplied results in that number are called the factor pairs of that number. To find the factor pairs of 432 follow the procedure given below:
1 x 432 = 432
2 x 216 = 432
3 x 144 = 432
4 x 108 = 432
6 x 72 = 432
8 x 54 = 432
9 x 48 = 432
12 x 36 = 432
16 x 27 = 432
18 x 24 = 432
The factor pairs of 432 are:
(1, 432)
(2, 216)
(3, 122)
(4, 108)
(6, 72)
(8, 54)
(9, 48)
(12, 36)
(16, 27)
(18, 24)
Similarly, negative factor pairs of 432 can also be found. the negative pairs are nothing but the positive factor pairs with a negative sign.
Factors of 432 Solved Examples
Let us solve some examples related to the factors of 432 to have a better understanding of the concept.
Example 1
Ana sent 432 candies to 12 children. Determine how many candies each child will get.
Solution
Total number of candies = 432
Total number of children = 12
Candies each will get = $\dfrac{432}{12}$
Candies each child will get = 36
Example 2
List down the negative factor pairs of 432.
Solution
Negative factor pairs of 432 are given as:
(-1, -432)
(-2, -216)
(-3, -122)
(-4, -108)
(-6, -72)
(-8, -54)
(-9, -48)
(-12, -36)
(-16, -27)
(-18, -24)
Images/mathematical drawings are created with GeoGebra.
