JUMP TO TOPIC
Factors of 48: Prime Factorization, Methods, and Examples
The factors of 48 are the specific numbers that result in 48 when multiplied together in pairs. In other words, the factors of 48 can be described as follows:The factors of 48 are the specific numbers that divide the number 48 exactly and leave zero in the remainder.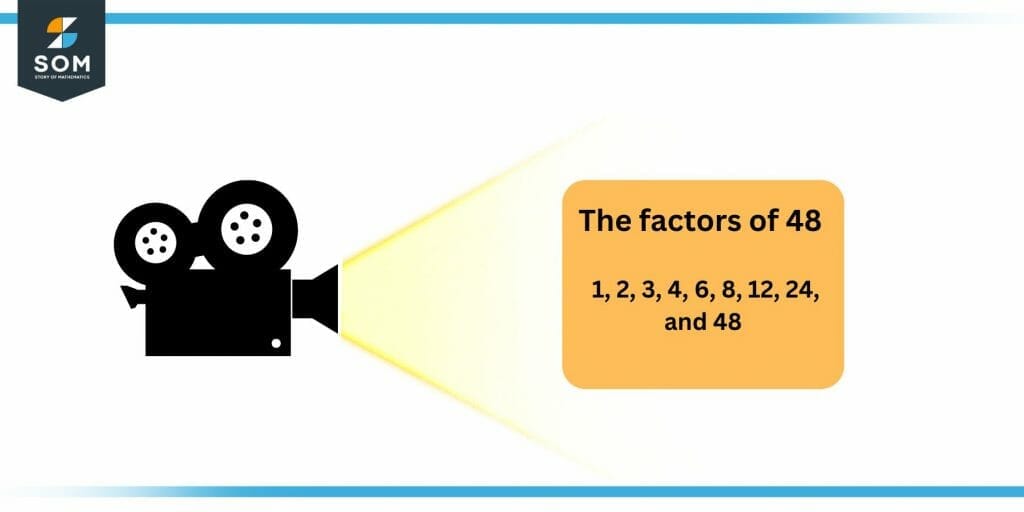
Figure 1 – All possible factors of 48
What Are the Factors of 48?
The factors of 48 are 1, 2, 3, 4, 6, 8, 12, 24, and 48.48 is an even composite number that has only 10 factors in total. All the above numbers are perfect divisors of 48. When 48 is divided by these numbers, it is divided completely with no remainder.Points To Ponder
- The number 1 is the smallest factor of every number. So, 1 is a factor of 48.
- The number itself is the largest factor of that number. Hence, 48 is a factor of 48.
- The number 2 is a factor of every even number.
How To Calculate the Factors of 48?
To calculate the factors of 48, start dividing 48 by the smallest natural number that divides 48 exactly and proceed with consecutive natural numbers up to the number 48.Divide 48 by the smallest natural number i.e., 1.\[\dfrac{48}{1} = 48\]As it has divided 48 without any remainder, 1 is a factor of 48.Now, divide 48 by the smallest even prime number i.e., 2.\[\dfrac{48}{2} = 24\]As it has again divided 48 completely, so 2 is also a factor of 48.Again divide 48 by the smallest odd prime number i.e., 3.\[\dfrac{48}{3} = 16\]As 3 has divided 48 exactly. So, 3 is too a factor of 48.For getting more factors, divided 48 by natural numbers that exactly divide 48 and leave zero remainders as shown below:\[\dfrac{48}{4} = 12\]\[\dfrac{48}{6} = 8\]\[\dfrac{48}{8} = 6\]\[\dfrac{48}{12} = 4\]\[\dfrac{48}{16} = 3\]\[\dfrac{48}{24} = 2\]\[\dfrac{48}{1} = 48\]Hence, all the above numbers exactly divide 48 without leaving any remainder, so all the above numbers are factors of 48.If we divide the number 48 by any numbers other than 1, 2, 3, 4, 6, 8, 12, 16, 24, and 48, it leaves a remainder; hence, they are not the factors of 48.The method described above is called the division method to find factors of a number.Basic Information
- All divisors of 48 are also factors of 48 irrespective of prime or composite numbers.
- Factors of 48 can never be in fractions or decimals.
- Factors of 48 can be positive as well as negative.
- If the last digit of any number is an even number, it is divisible by 2 exactly. For example, the last digit of 48 is 8 which is an even number.
- If the sum of digits of any number is divisible by 3, the number is also divisible by 3. For example, the sum of digits of the number 48 is 12, and 12 is divisible by 3. Hence 48 is also divisible by three.
Factors of 48 by Prime Factorization
To find factors of 48 by the prime factorization method, divide 48 by the smallest prime number which divides 48 exactly without any remainder. Then the quotient is again divided by the smallest prime number and the procedure continues until we get the quotient as 1.Following is the method to calculate factors of 48 by prime factorization.First, divide 48 by the smallest prime number which is 2.\[\dfrac{48}{2} = 24 \]The quotient 24 is a composite number and can further be divided by 2.\[\dfrac{24}{2} = 12\]Again 12 is a composite number that can be further divided by 2.\[\dfrac{12}{2} = 6 \]Now 6 again can be divided further by 2.\[\dfrac{6}{2} = 3\]3 further can be divided by 3.\[\dfrac{3}{3} = 1 \]The quotient 1 cannot be divided further.Therefore, the prime factorization of 48 can be stated as:Prime Factorization = 2 × 2 × 2 × 2 × 3
Prime Factorization of 48 can also be written as:48 = $2^4$ x 3
Prime Factorization method of 48 is also shown in the following Figure 1.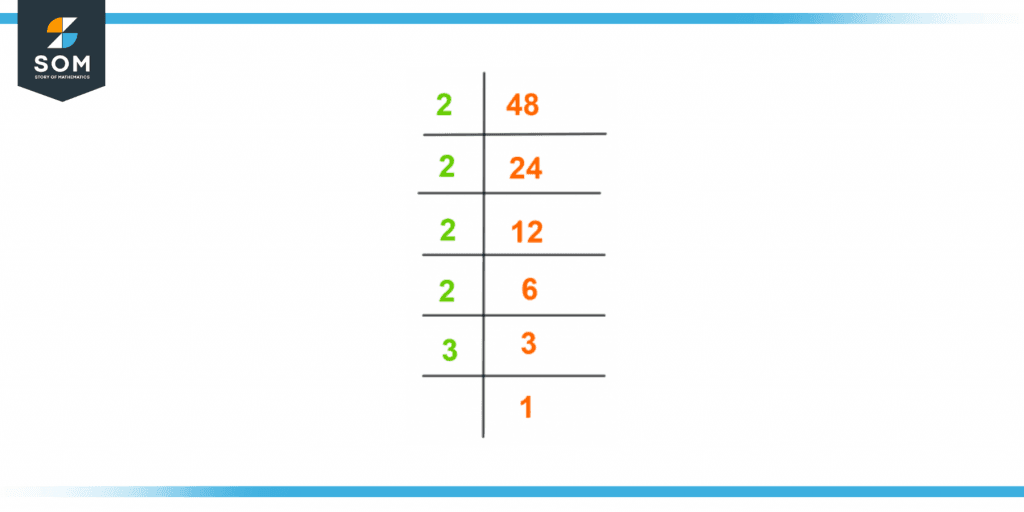
Figure 2 – Prime factorization of 48
Important Definitions
- If any number has only two divisors that is 1 and the number itself, it is called a prime number.
- If the factors of a number are prime numbers, then the factors are called prime factors.
- Prime factorization is a method to write a number as a product of all of its prime factors.
Factor Tree of 48
A factor tree is a way to express the factors of a number, specifically the prime factorization of a number in which each branch in the tree splits into factors.Once the factor at the end of the branch is a prime number, and the other is a composite number. Divide the composite number again unless the only two factors remain, that a prime number and 1 so the branch stops.If we write 48 into multiples, it would be 48 = 2 × 24.On dividing 24 into its multiples, it would be 24 = 2 × 12.Dividing further 12 into its multiples. It would result in 12 = 2 × 6.On further dividing 6 into its multiple factors, it would be 6 = 2 × 3By splitting 3 further and writing its multiples, it would be 3 = 3 × 1Altogether expressing the number in terms of prime factors would be:2 x 2 x 2 x 2 x 3
Factor Tree of 48 is also shown in Figure 2.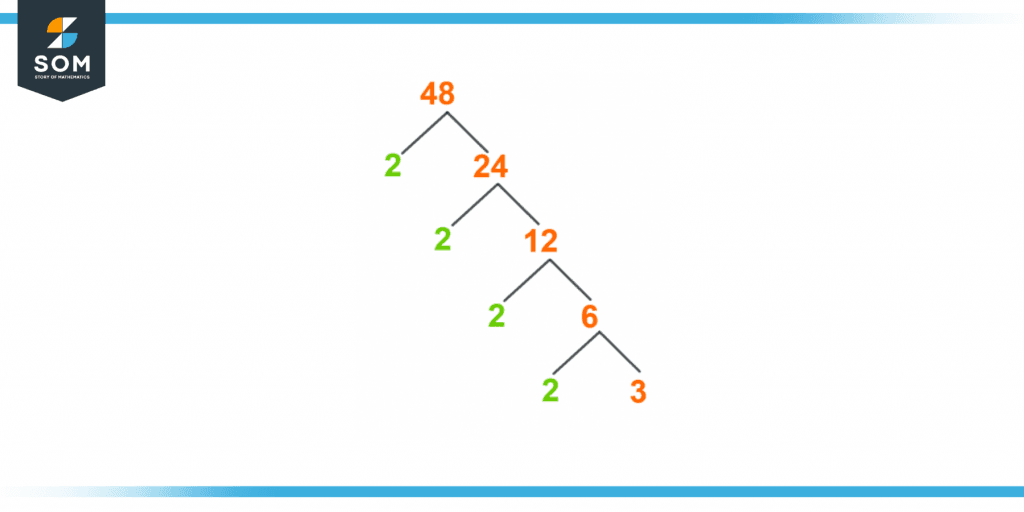
Figure 3 – Factor tree of
Factors of 48 in Pairs
A set of two integral numbers, whose product gives us the number 48 are called factors of 48 in pairs.Pair Factors are a pair of numbers that are multiplied by each other and give the result of 48 itself. Following are the pair factors of 48.1 x 48 = 48
2 x 24 = 48
3 x 16 = 48
4 x 12 = 48
6 x 8 = 48
8 x 6 = 48
12 x 4 = 48
16 x 3 = 48
24 x 2 = 48
48 x 1 = 48
As there are 10 factors of 48. So, these factors can be written in pairs as follows:(1, 48)
(2, 24)
(3, 16)
(4, 12)
(6, 8)
(8, 6)
(12, 4)
(16, 3)
(24, 2)
(48, 1)
48 also can have two negative numbers as pair factors. For example:(-12) x (-4) = 48
(-6) x (-8) = 48
(-3) x (-16) = 48
Hence, the following are some examples of negative pair factors of 48:(-12 , -4)
(-6 , -8)
(-3, -16)
So, it can be derived that the product of all factors of 48 in its negative form, gives the result 48. So, all are called negative pair factors of 48.Important Facts About 48
- 48 is a composite number.
- 48 is also an even number.
- 48 has only 2 prime factors.
- The smallest even prime number is a factor of 48.
- The smallest odd prime number is also a factor of 48
- 48 has 10 divisors.
- 48 has 10 positive factors and 10 negative factors.
- 24 is the biggest factor of 48 excluding 48 itself.
Factors of 48 Solved Examples
Example 1
Jenifer has been given a question in her homework to find the common factors of 24 and 48. What method should she adopt to find the solution to the given question? How will she find the greatest common factor?Solution
Janifer knows the method to find factors of any number by division. She will find all the factors of 24 and 48 which are as follows:Factors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24Factors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24, and 48.It is visible from the factors of 24 and 48 that common factors are: 1, 2, 3, 4, 6, 8, 12, and 24.From the factors, it is quite clear that the Greatest Common Factor (G.C.F) of 24 and 48 is 24.Example 2
Joseph has bought 48 candies packet for his kid named Peter. Peter has eaten all the candies in merely 12 days. Find how many candies Peter has eaten per day.Solution
To find out the candies eaten by Peter on daily basis, we have to find out that12 x x = 48
Now let’s find the missing factor “x”.Using the multiplication fact, we know that12 x 4 = 48
Hence, Peter has eaten 4 candies per day and consumed the packet in 12 days.Example 3
Which of the following statement is False about factors of 48?- The smallest even number is a factor of 48.
- The smallest odd number is a factor of 48.
- 48 has only two prime factors
- 48 has no composite factors.
