JUMP TO TOPIC
Factors of 500: Prime Factorization, Methods, Tree, and Examples
Factors of 500 include the numbers that perfectly divide 500 having the whole number as quotients and zero as the remainder. If the residue is a non-zero number, the divisor will not be a factor of 500.
Figure 1 – All possible Factors of 500
2 x 250= 500
In this article, we will learn about the factors of 500. After grasping this concept, you will find prime factorization, prime numbers, and factor pairs of a number by using both positive and negative factors and a factor tree. Ultimately there are some explained examples for better understanding.What Are the Factors of 500?
The factors of 500 are 1, 2, 4, 5, 10, 20, 25, 50, 100, 125, 250, and 500. These integers divide 500 by leaving the remainder zero.500 has twelve factors in total. By multiplying these integers in pairs such that the product is equal to 500. Such numbers are stated to comprise the factors of 500.How To Calculate the Factors of 500?
You can find the factors of 500 by using the rules of divisibility that demand the remainder to be zero for a number to be considered as a factor of the given number.To find factors of 500 start dividing it by different numbers and check whether the remainder is zero or not, If the remainder is zero then that number will be considered as the factor of 500 otherwise it wouldn’t be considered as a factor of 500.Let’s dive into the ocean of factors of 500. Starting with the number 1 as it is a factor of every whole number. Dividing 500 by 1 results in 500 with no remainder as:\[\frac {500}{1}= 500\] As a result, 1 will be included in every list of factors.500 is an even number so it can easily be divided by 2. Dividing 500 by 2 gives:\[\frac {500}{2}= 250\]This means 2 and 250 are also the factors of 500 because both divide 500 entirely and the remainder is zero in both cases.Dividing 500 by 3 results in a quotient which is 166 :\[\frac {500}{3}= 166.6\] The remainder is 2, which is a non-zero number so 3 is not a factor of 500.Now, divide 500 by 4 gives:\[\frac {500}{4}= 125\] The remainder is zero so 4 and 125 are also the factors of 500.Dividing 500 by 6 again results in a decimal number which cannot be a factor of 500.\[\frac {500}{6}= 83.33\] The remainder is 6. Six attends to be a non-zero number. 6 is not a factor of 500.Dividing 500 by 10 gives:\[\frac {500}{10}= 50\]The remainder is zero, so 10 and 50 are also the factors of 500.Dividing 500 by 20 gives:\[\frac {500}{20}= 25\]The remainder is zero, so 20 and 25 are also the factors of 500.Dividing 500 by 100 gives:\[\frac {500}{100}= 5\]The remainder is zero, so 100 and 5 are also the factors of 500.The last factor will be the number 500 itself because every number divides itself fully.\[ \frac{500}{500} = 1 \]By the above steps, we obtain the factors of 500 as given below:Factors of 500 : 1, 2, 4, 5, 10, 20, 25, 50, 100, 125, 250, 500 And negative factors of 500 are:Negative Factors of 500 : -1, -2, -4, -5, -10, -20, -25, -50, -100, -125, -250, -500Some key points for your more proper understanding are provided below:- If the number has an odd number of factors, it is a perfect square.500 has twelve factors 12 is an even number, so it is not a perfect square.
- A number having more than two factors is known as a composite number.
Factors of 500 by Prime Factorization
Scribbling a number as a product of its prime factors is called prime factorization. By way of explanation, prime factors are factors of a number that are prime numbers.The core objective of prime factorization is to determine the prime factors of a number. By multiplying those prime factors in a way that their product is the same as the number whose factors we are finding.2 and 5 are prime factors of 500. The prime factorization of 500 is given as:2 x 2 x 5 x 5 x 5 = 500
Prime factors are 2 and 5, but we need to repeat number 2 twice and number 5 thrice to obtain the required product.It can also be noted as: \[ 2^2 \times 5^3= 500 \]Figure 1 shows the prime factorization of 500 below: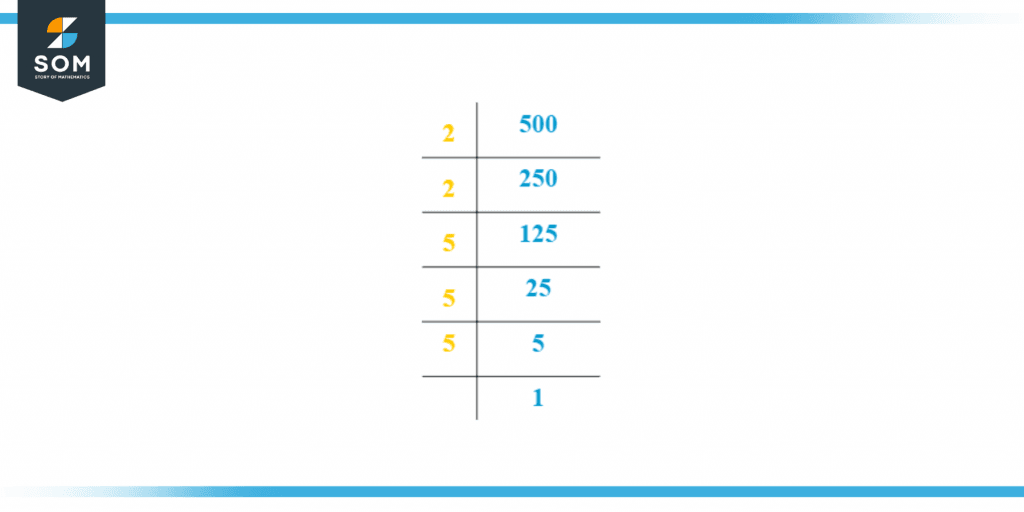
Figure 2 – Prime factorization of 500
- Factor Tree.
- Division Method.
Factor Tree of 500
The factor tree is a way of expressing the prime factorization of a number. It consists of the factored number at the top, it splits into branches, and each branch contains the factors of the given number. A factor tree is a pictorial representation of prime factors.The factor tree of 500 can be illustrated as: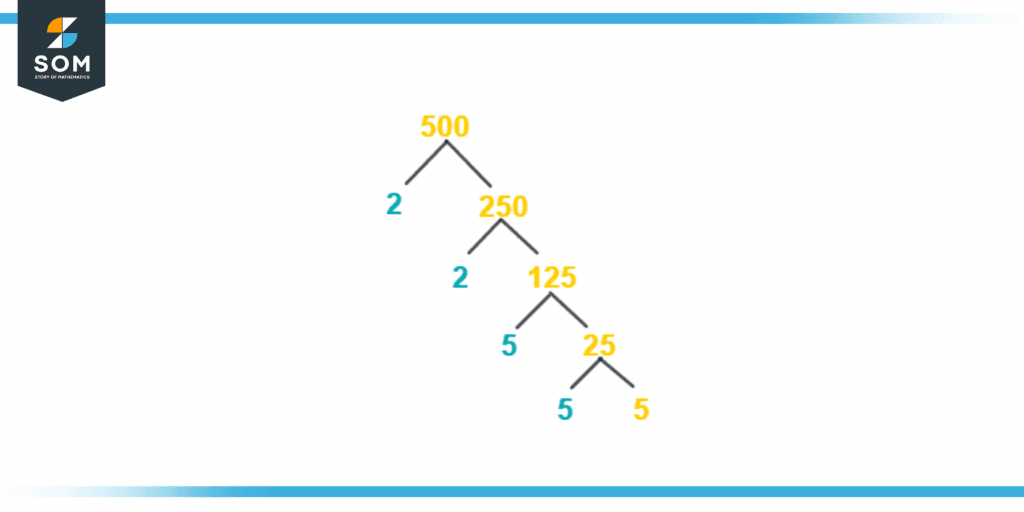
Figure 3 – Factor tree of 500
Factors of 500 in Pairs
Writing factors of a number in pairs so that the product of those particular factors in pairs must be equal to the number itself is called the factor pairing method. The resulting sets of factors are called factor pairs.1 x 500= 500
2 x 250= 500
4 x 125= 500
5 x 100= 500
10 x 50= 500
20 x 25= 500
By looking at the above multiplication we will write the factor pairs for 500 as:(1, 500)
(2, 250)
(4, 125)
(5, 100)
(10, 50)
(20, 25)
Negative factor pairs of 500 are found as:-1 x -500= 500
-2 x -250= 500
-4 x -125= 500
-5 x -100= 500
-10 x -50= 500
-20 x -25= 500
When a negative sign is multiplied by a negative sign their product is always positive. Negative factor pairs for 500 are (-1, -500), (-2, -250), (-4, -125), (-5, -100), (-10, -50), and (-20, -25).Factors of 500 Solved Examples
Let’s solve some examples of factors of 500 for better understanding and practice.Example 1
Harry owns a bookshop. A customer placed an order of 5 books. The cost of one book is $100. Find the total cost of 5 books.Solution
(5,100) is a factor pair of 500Cost of one book = $100
Total books = 5
Total cost of 5 books = 5 x 100= 500
The total cost of 5 books =$500
Example 2
Find the common factors of 500 and 94.Solution
Factors of 500 : 1, 2, 4, 5, 10, 20, 25, 50, 100, 125, 250, 500 Factors of 94 : 1,2,47, 94 Common factors of 500 and 94 are 1 and 2.Example 3
Find the sum of the Even factors of 500.Solution
Factors of 500 are 1, 2, 4, 5, 10, 20, 25, 50, 100, 125, 250, & 500.Even numbers are those that are divisible by 2 Even Factors of 500 are 2, 4, 10, 20, 50, 100, 250, and 500.Sum of Even Factors of 500:Sum = 2+4+10+20+50+100+250+500
Sum =936
So the sum is equivalent to 936.Example 4
Peter has 500 candies. He has to divide them among 4 friends. How much will each friend get?Solution
Total candies = 500
Number of friends = 4
\[\frac {500}{4}= 125\]4 and 125 are factors of 500.Images/mathematical drawings are created with GeoGebra.
