Factors of 595: Prime Factorization, Methods, and Examples

595 has a total of 8 factors which makes it a composite number. The list includes  1, 5, 7, 17, 35, 85, 119 and 595 itself. The factors of a number are always whole numbers. They can never be decimals or fractions. 

Every number ending at 5 has the number 5 as its factor.

Factors of 595

Here are the factors of number 595.

Factors of 595:  1, 5, 7, 17, 35, 85, 119 and 595

Negative Factors of 595

The negative factors of 595 are similar to its positive aspects, just with a negative sign.

Negative Factors of 595: -1, -5, -7, -17, -35, -85, -119 and -595

Prime Factorization of 595

The prime factorization of 595 is the way of expressing its prime factors in the product form.

Prime Factorization: 5 x 7 x 17

In this article, we will learn about the factors of 595 and how to find them using various techniques such as upside-down division, prime factorization, and factor tree.

What Are the Factors of 595?

The factors of 595 are  1, 5, 7, 17, 35, 85, 119, and 595. These numbers are the factors as they do not leave any remainder when divided by 595.

The factors of 595 are classified as prime numbers and composite numbers. The prime factors of the number 595 can be determined using the prime factorization technique.

How To Find the Factors of 595?

You can find the factors of 595 by using the rules of divisibility. The divisibility rule states that any number, when divided by any other natural number, is said to be divisible by the number if the quotient is the whole number and the resulting remainder is zero.

To find the factors of 595, create a list containing the numbers that are exactly divisible by 595 with zero remainders. One important thing to note is that 1 and 595 are the 595’s factors as every natural number has 1 and the number itself as its factor.

1 is also called the universal factor of every number. The factors of 595 are determined as follows:

\[\dfrac{595}{1} = 595\]

\[\dfrac{595}{5} = 119\]

\[\dfrac{595}{7} = 85\]

\[\dfrac{595}{17} = 35\]

[\dfrac{595}{35} = 17\]

\[\dfrac{595}{85} = 7\]

\[\dfrac{595}{119} = 5\]

\[\dfrac{595}{595} = 1\]

Therefore, 1, 5, 7, 17, 35, 85, 119, and 595 are the factors of 595.

Total Number of Factors of 595

For 595, there are 8 positive factors and 8 negative ones. So in total, there are m factors of 595. 

To find the total number of factors of the given number, follow the procedure mentioned below:

1. Find the factorization/prime factorization of the given number.
2. Demonstrate the prime factorization of the number in the form of exponent form.
3. Add 1 to each of the exponents of the prime factor.
4. Now, multiply the resulting exponents together. This obtained product is equivalent to the total number of factors of the given number.

By following this procedure, the total number of factors of 595 is given as:

Factorization of 595 is 5 x 7 x 17.

The exponent of 5, 7, and 17 is 1.

Adding 1 to each and multiplying them together results in 16.

Therefore, the total number of factors of 595 is 16. 8 are positive, and 8 factors are negative.

Important Notes

Here are some essential points that must be considered while finding the factors of any given number:

• The factor of any given number must be a whole number.
• The factors of the number cannot be in the form of decimals or fractions.
• Factors can be positive as well as negative.
• Negative factors are the additive inverse of the positive factors of a given number.
• The factor of a number cannot be greater than that number.
• Every even number has 2 as its prime factor, the smallest prime factor.

Factors of 595 by Prime Factorization

The number 595 is a composite number. Prime factorization is a valuable technique for finding the number’s prime factors and expressing the number as the product of its prime factors.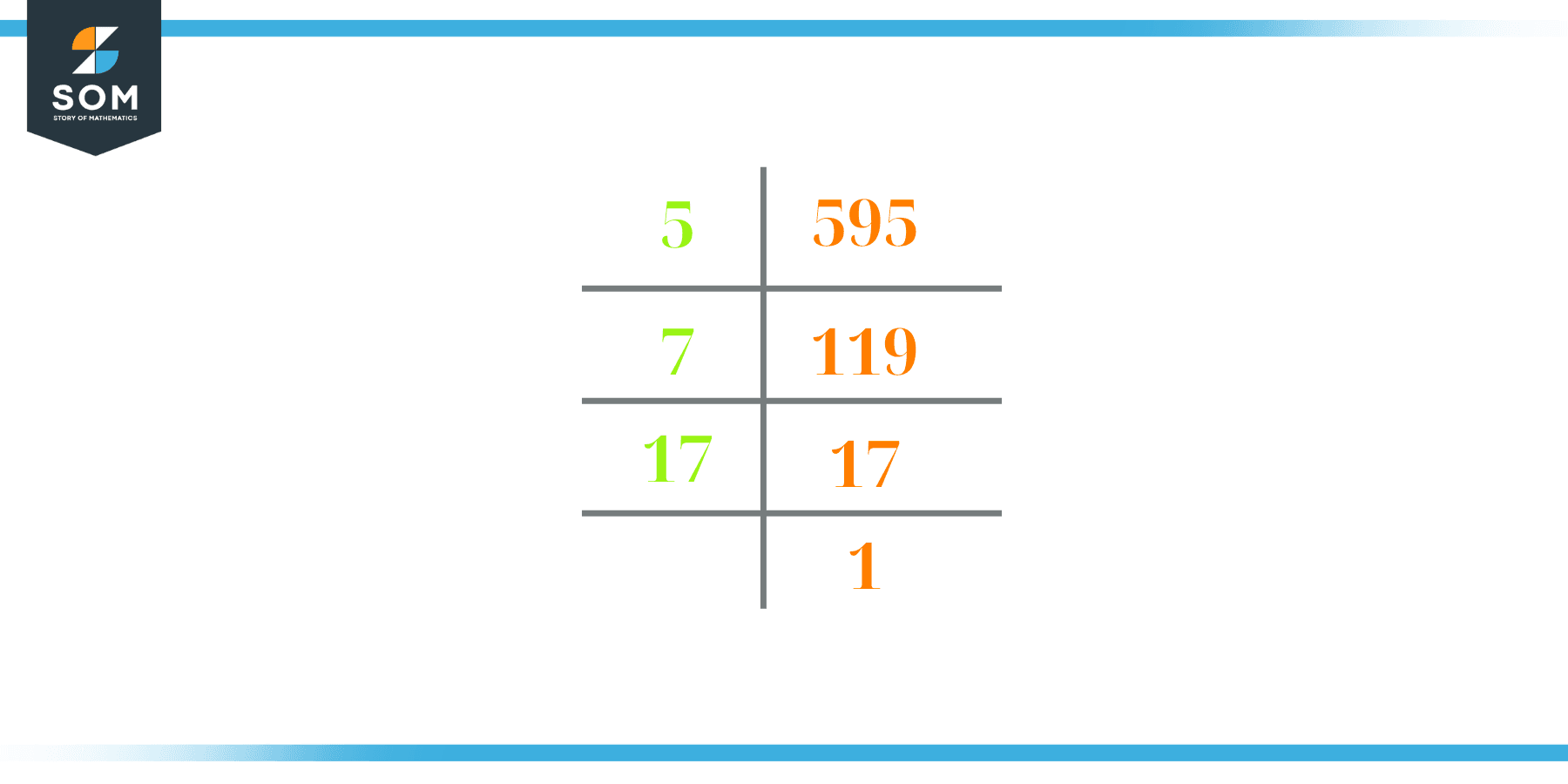

Before finding the factors of 595 using prime factorization, let us find out what prime factors are. Prime factors are the factors of any given number that are only divisible by 1 and themselves.

To start the prime factorization of 595, start dividing by its most minor prime factor. First, determine that the given number is either even or odd. If it is an even number, then 2 will be the smallest prime factor.

Continue splitting the quotient obtained until 1 is received as the quotient. The prime factorization of 595 can be expressed as:

595 =5 x 7 x 17

Factors of 595 in Pairs

The factor pairs are the duplet of numbers that, when multiplied together, result in the factorized number. Factor pairs can be more than one depending on the total number of factors given.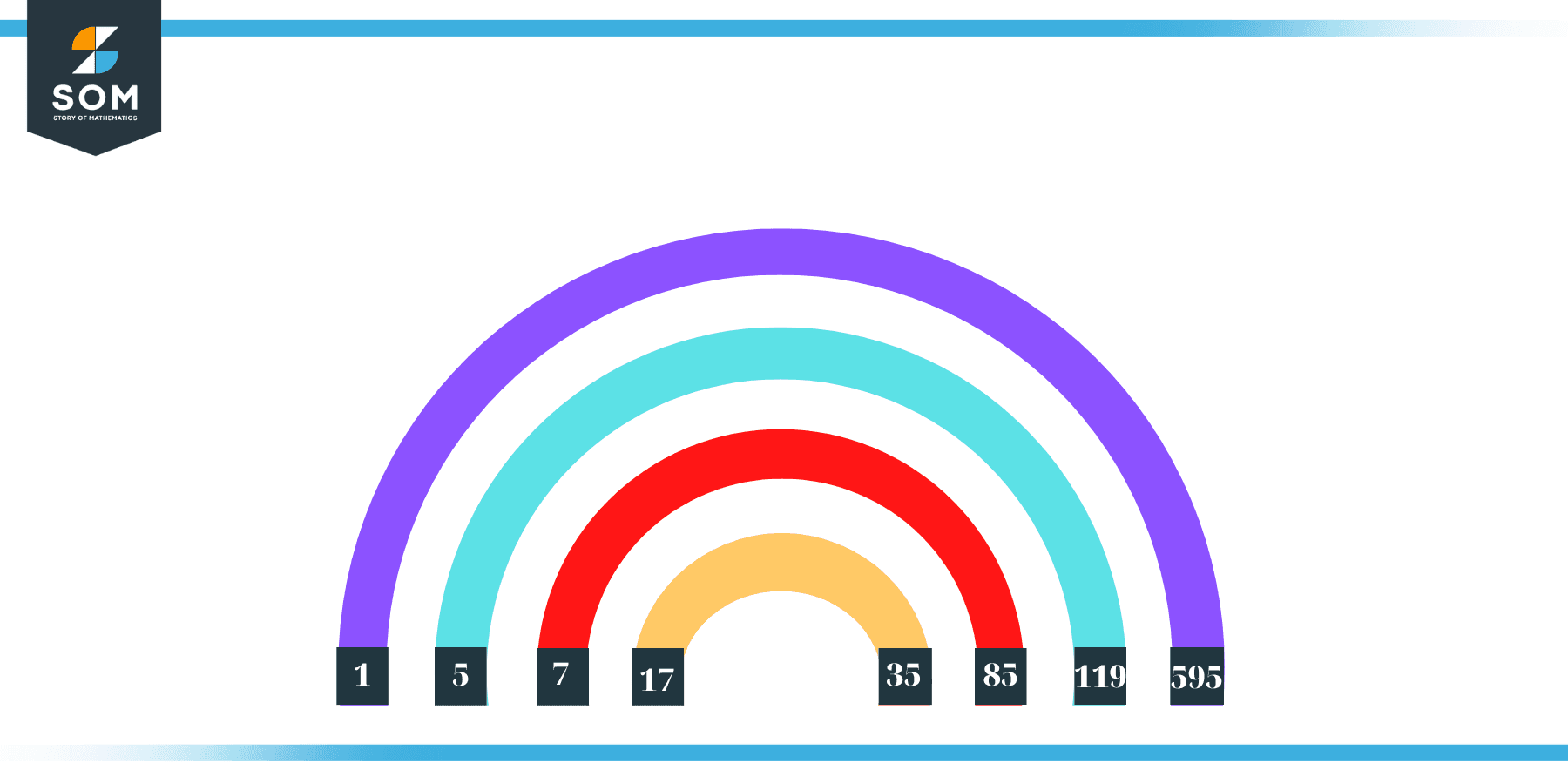

For 595, the factor pairs can be found as:

1 x 595 = 595

5 x 119 = 595

7 x 85 = 595

17 x 35 = 595

The possible factor pairs of 595 are given as (1, 595),(5, 119),(7, 85), and (17, 35).

All these numbers in pairs, when multiplied, give 595 as the product.

The negative factor pairs of 595 are given as:

-1 x -595 = 595

-5 x -119 = 595

-7 x -85 = 595

-17 x -35 = 595

It is important to note that in negative factor pairs, the minus sign has been multiplied by the minus sign, due to which the resulting product is the original positive number. Therefore,  -1, -5, -7, -17, -35, -85, -119 and -595 are called negative factors of 595.

The list of all the factors of 595, including positive as well as negative numbers, is given below.

Factor list of 595:  1,-1, 5,-5,7, -7, 17,-17, 35,-35, 85,-85, 119,-119 , 595, and -595

Factors of 595 Solved Examples

To better understand the concept of factors, let’s solve some examples.

Example 1

How many factors of 595 are there?

Solution

The total number of Factors of 595 is 16.

Factors of 595 are 1, 5, 7, 17, 35, 85, 119 and 595.

Example 2

Find the factors of 595 using prime factorization.

Solution

The prime factorization of 595 is given as:

595 $\div$ 5 = 119

119 $\div$ 7 = 17 

17 $\div$ 17 = 1 

So the prime factorization of 595 can be written as:

 5 x 7 x 17= 595

Factors of 594|Factors List| Factors of 596