Factors of 625: Prime Factorization, Methods, Tree, and Examples

Factors of 625 can be found when any two numbers multiplied together give the number 625 as a product or when the number 625 is divided by another number and it provides zero remainders. These numbers are called factors of the number 625.

Figure 1 – All possible factors of 625

Every number has both positive factors and negative factors. We can exclude the negative factors if we want to. A factor always has to be a whole number and never in fraction or decimal format.

The number 625 has in total 10 factors, out of which only 5 factors are positive. 

In this article, you can learn about all of the Prime Factors, Factor trees, fun facts, and tricks to solve questions related to the factors of 625.

What Are the Factors of 625?

The complete factors of 625 are 1, 5, 25, 125, and 625 as the integers that divide 625 to give 0 as the reminder and whole numbers as quotients. All these numbers are listed as factors of 625.

Any number that ends with the number 5 will have 5 as a factor. 625 is an odd and composite number. So by dividing the number 625 by other numbers we can form the list of 625.

625 = 1, 5, 25, 125, 625 

How To Calculate the Factors of 625?

You can calculate all of the factors of 625 by dividing 625 by different integers. The integers that will completely divide 625 are the factors of 625.

The factors of 625 using this method are given as:

\[ \dfrac{625}{1}=625\] remainder = 0

\[ \dfrac{625}{5}=125\] remainder = 0 

\[ \dfrac{625}{25}=25\] remainder = 0

\[ \dfrac{625}{125}=5\] remainder = 0

\[ \dfrac{625}{625}=1\] remainder = 0

First, we have divided the number 625 by the smallest natural number which is 1. From the above division, it has been concluded that 1 is the Factor of 625. 

Repeating the above process for all the natural numbers until 625 yields all the possible factors of 625. This is the main method to find the factors of 625 or any number. This is called the basic division method.

But this process can be lengthy and time-consuming so here are some tips to follow while finding the factors of 625:

1. 625 is a composite number and has more than two factors.
2. 625 is an odd number therefore 2 can never be its factor.
3. 625 is the multiple of 5 so, 5 is the factor of 625.
4. 625 is a square of 25. So, 25 is also the factor of 625.
5. The prime factorization of 625 is expressed as $5^4$. Therefore, 5 x 5 x 5 = 125 . 125 is also the factor of 625.

Keeping all these points in view, the factor list of 625 is given as:

625 = 1, 5, 25, 125, 625 

Similarly, the list of all of the negative  factors of 625 is given as:

625 = -1,- 5,- 25, -125,- 625 

We can also determine the factors of 625 by finding any two numbers whose product will give us 625 as an answer.

1 x 625 = 625 

This is called the multiplication method or factor pairing. It is an alternative for finding Factors.

Here are some Fun Facts about the number 625 and its factors:

1.  625 is also a perfect fourth power of 5.
2. The Prime Factorization exponent of 625 is 4.
3. There are only two-three digits factors i.e. 125 and 625.
4. 625 and its additive inverse -625 both are the factors of 625.
5. Along with every other number, 1 is also a factor of 625.

Factors of 625 by Prime Factorization

Prime factors of 625 are all those numbers that can only be divided by 1 and that number itself. Hence these factors, when multiplied altogether, give 625 as the product. It can be done in 2 different ways.

To find the prime factors you can follow the steps given below:

\[ \dfrac{625}{5}=25\] remainder = 0

\[ \dfrac{125}{5}=125\] remainder = 0

\[ \dfrac{25}{5}=5\] remainder = 0

\[ \dfrac{5}{5}=1\] remainder = 0

We will choose the smallest prime number factor i.e. 5. Then we will divide 625 by 5. We will repeat the process until we get 1 as a quotient. So we will keep on dividing till quotient 1 is obtained. Note that a remainder indicates that the number is not a factor of the given number. 

Note that zeros and 1s are not considered prime numbers so we will not include them in the factorization.

The prime factorization of 625 is expressed as:

5 x 5 x 5 x 5 = 625 

Prime factorization 0f 625 is also shown as:

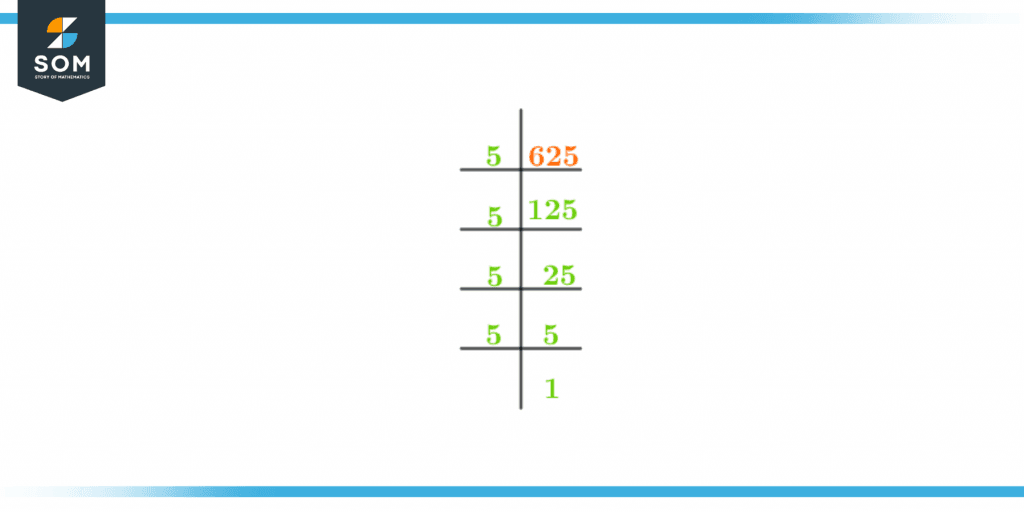
Figure 2 – Prime factorization of 625

Factor Tree of 625

It is a way to illustrate the prime factors of a number and the factors of those numbers too. We can make a factor tree to understand the prime factorization even better. For that, we must clarify our concept of prime factors.

625 has only one prime factor which is 5 and it has been raised to power 4.

The diagram given below in figure 2 is called a factor tree.

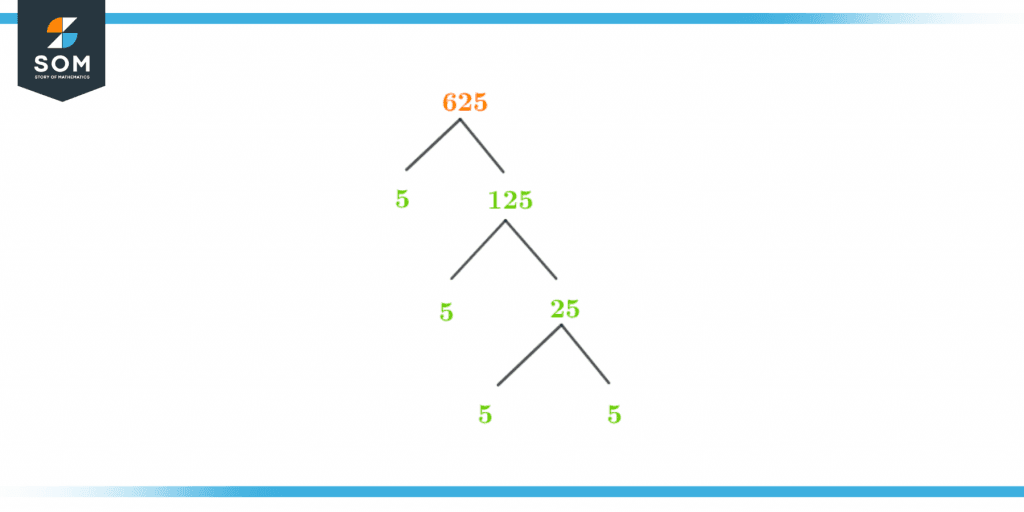
Figure 3 – Factor Tree of 625

Factors of 625 in Pairs

A factor pair is the group of two numbers that gives that certain factored number as the product. For the number 625, we will find factor pairs by multiplying any two factors which give 625 as an answer. For positive factors, we can find pairs as:

1 x 625 = 625 

5 x 125 = 625 

25 x 25 = 625 

Note that each number when multiplied by the other number gives 625 as the result which indicates that they are the positive factor of 625.

Now for the negative factors of 625, we can also find the factor pairs as: 

-1 x -625 = 625 

-5 x -125 = 625 

-25 x -25 = 625 

Since two times minus will cancel out each other so we will get the negative factor pairs of 625.

The factor pairs of 625 are given as:

Positive Factor Pair of 625 are (1, 625), (5, 125), (25, 25)

Negative Factor Pair of 625 are (-1,- 625), (-5, -125), (-25, -25) 

Factors of 625 Solved Examples

Example 1

What are the common factors of 625 and 25?

Solution

As the Factors of 25 are:

25 = 1, 5,25 

Whereas, the factors of 625 are:

625 = 1, 5, 25, 125, 625 

So the common factors of 25 and 625 are 1, 5, and 25.

Example 2

List all of the negative factors of 625 and the prime factors.

Solution

Factors of 625 are the numbers that divide to give zero remainders when 625 is the dividend.

As Negative factors of 625 are:

625 = -1, -5, -25, -125, -625 

So the Prime Factors of 625 can be written as:

5 x 5 x 5 x 5 = 625 

Example 3

Miss Julia is a teacher. She has 25 students in her class. For an art project, she has 625 pencils. Can you help Miss Julia divide the 625 pencils among her class so that everyone gets an equal number of pencils?

Solution

We will use the Factors concept to find the number of pencils given to each student. As 625 is a multiple of 25 so we can divide the pencils equally by finding the factor pair of 625 which includes 25 which is

25 x 25 = 625 

Hence, Miss Julia will give each student 25 pencils for the art project so that every student will get an equal number of pencils.

Images/mathematical drawings are created with GeoGebra.

Factors List