JUMP TO TOPIC
Factors of 63: Prime factorization, Methods, Tree, and Examples
Factors of 63 refer to the numbers that, when multiplied together, produce a result of 63, or they are the numbers by which 63 may be divided. Therefore, if a number divides 63 with a remainder of 0, it is referred to as a factor.

Figure 1 – All possible Factors of 63
To check the factors of the number you are looking for, list all the integers that are less than or equal to the number you are looking for. The numbers for 63, for instance, will fall between 1 and 21. In such a case, dividing each of them will yield the answer.
The fact that two is the factor of all numbers is an intriguing fact about factors. However, division and multiplication can determine a number’s factors.
Nevertheless, there are numerous approaches to finding integer factors. Even more straightforward methods exist for determining a number’s components. Simply divide the number by itself until the remainder equals zero, at which point the quotient and the divisor are considered to be factors of the given number.
Let’s consider one of these cases as an example:
\[ \frac{63}{3} = 21\]
As a result, the solution, as well as the divisor, are both considered to be factors. They are collectively referred to as factor pairs, i.e. (3, 21).
This article will provide you with the greatest explanation it can of all the information about the factors of 63 for a clearer understanding. It includes simple solutions, wonderful examples, and interesting information about the number 63.
What Are the Factors of 63?
The factors of 63 are 1, 3, 7, 9, 21, and 63. 63 has more than two factors since it is a composite number.
In total there are six factors of 63. The values that divide the number 63 perfectly without producing a remainder are called the factors of 63.
How To Calculate the Factors of 63?
You can calculate the factors of 63 using a basic division procedure. Let’s get going.
Divide 63 by the smallest divisor you can find, which is 1. In light of this, one of the factors of 63 is 1. Then check the following whole number to see if it can divide 63 in half completely. The division will be as follow:
\[ \frac{63}{3} = 21\]
Thus, 3 is a factor of 63.
Once we get 1 as the answer after reaching the division when 63 is divided by itself, we can stop dividing by whole numbers. Because of this, we cannot use any more whole numbers.
Following are the factors of 63 by using the division method:
\[ \frac{63}{1} = 63 \]
\[ \frac{63}{3} = 21 \]
\[ \frac{63}{7} = 9 \]
\[ \frac{63}{9} = 7 \]
\[ \frac{63}{21} = 3 \]
\[ \frac{63}{63} = 1 \]
Thus, the factors of the number 16 are:
Factors: 1, 3, 7, 9, 21, 63
Let’s now concentrate on determining the factors through multiplication. Consider 63 to be the result of two whole numbers in every possible way. Every integer that appears in each of these products is one of the factors of 63.
For example:
1 x 62 = 63
21 x 3 = 8
7 x 9 = 8
Hence, 1, 3, 7, 9, 21, and 63 are the factors of 63.
Factors of 63 by Prime Factorization
The method of prime factorization, which entails figuring out which prime factors can multiply with one another to get the number as a product, is one way to express a specific number as the product of its prime factors.
To put it another way, it is a technique for determining or
representing a given integer as the sum of prime numbers. 1 and the number itself are the only two factors that make up a prime number.
The number 63 should have prime factors because it is a composite number. Let’s discover how to identify the primary factors. The first approach is to divide 63 by the smallest prime factor using let’s 2 as an example. We can move on to the next prime number, 3 because 63/2 will result in a fractional number when divided. Hence, it is not a factor. Let’s take a look at it:
\[ \frac{63}{2} = 31.5 \]
3 is a factor since the outcome of dividing 63 by it produces a complete number.
\[ \frac{63}{3} = 21 \]
We now go on to the following prime numbers, which are:
\[ \frac{21}{3} = 7 \]
The following prime number is 7, so we will continue till we get 1 as the answer.
\[ \frac{7}{7} = 1 \]
After the division process, we received the number 1. Ultimately, it keeps us from continuing. We can mathematically represent the prime factorization of 63 as:
\[ 2^{3} /times 7 = 63 \]
The prime factorization is shown in the diagram below as well.
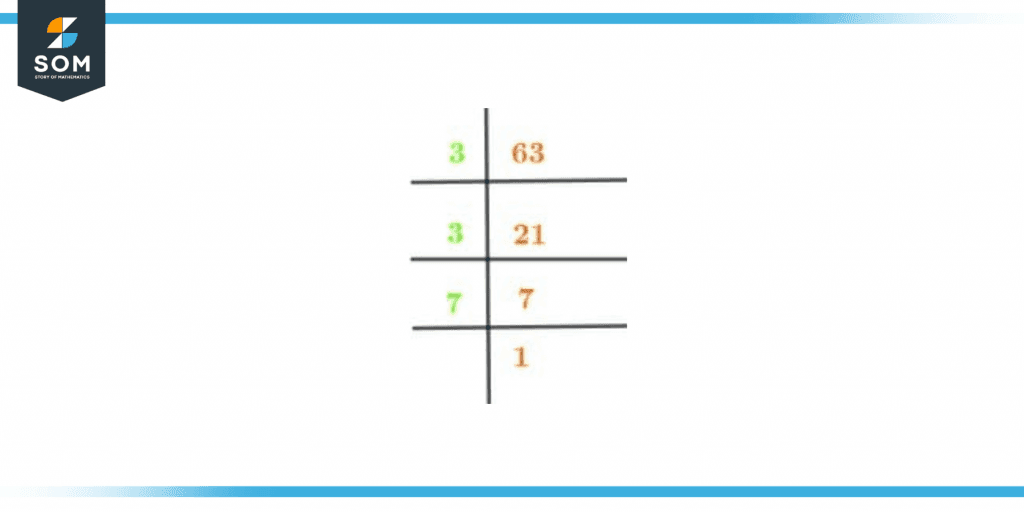
Figure 2 – Prime factorization of 63
Factor Tree of 63
Even a number’s factors can be expressed in a variety of ways. Expressing factors as a Factor Tree is only one of the many ways to graphically depict a number’s prime factors. The root of the factor tree is the actual number, and the branches that branch off from it stand in for factors until you reach the prime number.
Therefore, 3 and 7 are the prime factors of 63 as determined by prime factorization. Thus, 7 should be the last integer to be represented on the factor tree.
You can take a look at the Factor Tree of the number 63 below.
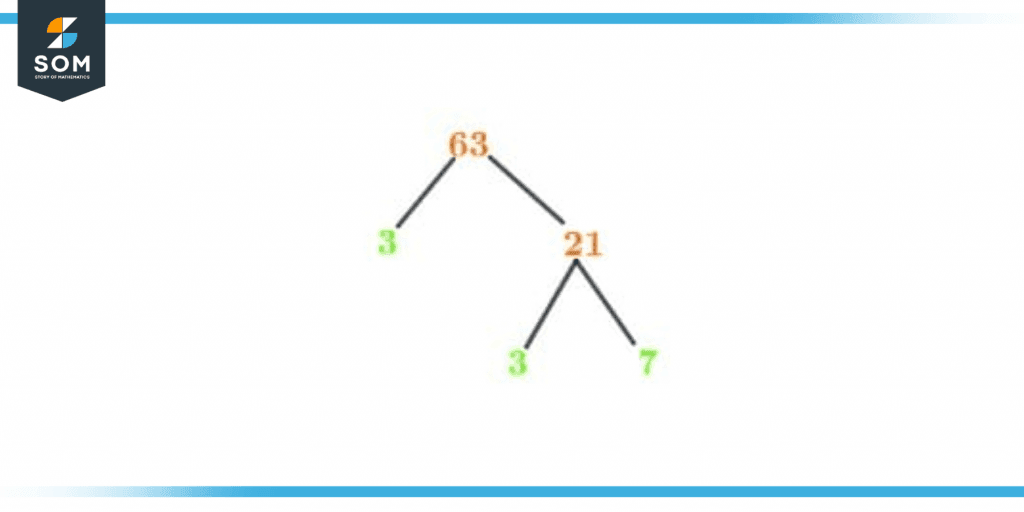
Figure 3 – Factor tree of 63
Let’s take a quick read of some really interesting fun facts about the number 63 are as follows:
- 63 is a highly cototient number, a deficient composite number, a Woodall number, and a third Delannoy number. Moreover, the total of all two-digit powers from 0 to 5 is 63.
- It is a number with a central octahedron. Also, 63 is the atomic number of europium.
- A machine gun known as Stoner 63 and 63 is the number of chromosomes discovered in a horse and donkey’s offspring.
- 63 is a game of cards that is well-known in Carleton County, New Brunswick.
- The quantity of groats in a guinea in pre-decimal British currency is 63. Furthermore, the country code for calls made directly to the Philippines from abroad.
- On April 20, 1987, during a double-overtime NBA playoff game between the Chicago Bulls and Boston Celtics, Michael Jordan set a record with 63 points.
- Schools that participate in NCAA Division I FCS are permitted to provide their football players a total of 63 full athletic scholarships in financial aid connected to their participation in athletics during a given season.
Factors of 63 in Pairs
Factor pairs of 63 are a pair of numbers that when multiplied together equal 63. The factors are as follows:
If 1 multiplied with 63 is 1, then (1, 63) is the pair factor of 63. Similarly, let’s look at more pairs:
3 x 21 = 63
7 x 9 = 63
9 x 7 = 63
21 x 3 = 63
Thus, (3, 21), (7,9), (9,7), and (21,3) are all factor pairs of 63.
These are the positive factor pairs of 63. To find out the negative factor pair, all you have to do is to reverse the signs. Let’s take a few examples of the negative factor pairs of the number 63:
-1 x -63 = -63
-3 x -21 = -63
-7 x -9 = -63
Hence, these are the negative factor pairs of 63. Keep in mind that you just have to reverse the signs of the positive factors to get the negative factors. The values that are multiplied in pairs to produce the number 63 are referred to as the pair factors of 63 such as (1, 63), (3, 21), and (7, 9).
Factors of 63 Solved Examples
Example 1
Find the common factors of 63 and 66.
Solution
The factors of 63 are:
Factors: 1, 3, 7, 9, 21, 63
Whereas the factors of 66 are:
Factors: 1, 2, 3, 6, 11, 22, 33, 66
Thus, the common factors of the numbers 12 and 16 are;
Common factors= 1, 3
Thus, the common factors of 63 and 66 are 1 and 3.
Example 2
In total, Sara has 63 cup set units. So that each unit is divided equally, she wants to pack it in cartons. For packing, she has two different size cartons available. A total of 14 units can fit in the first size, and only 7 units can fit in the second size.
Which kind of carton will Sara pick to load the cartons to the brim with units, leaving no space? What number of units will be kept in each carton?
Solution
Because there is no unit remaining, when 63 is divided by any of those two numbers that are 7 or 14, so, the result must be 0. Therefore, the quantity must be a factor of 63. 7 is a factor of 63 out of the two values given. As a result, Sara will pick cartons with a capacity of 7 units in the second size.
Divide 63 by 7 to get the number of units in each carton of the second size.
\[ \frac{63}{7} = 9 \]
All images/ mathematical drawings are created with GeoGebra.
