JUMP TO TOPIC
Factors of 72: Prime Factorization, Methods, Tree and Examples
All the numbers that perfectly divide the number 72 and do not leave any remainder are called the factors of 72.

Figure 1 – All possible factors of 72
This article will provide insight regarding the factors of 72 and how to find them by using various methods, including prime factorization and division methods. This article also explains the Factor Tree of 72, and Factors of 72 in Pairs with some examples.
What Are the Factors of 72?
The factors of 72 are as follows: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36 and 72. All the numbers mentioned above are perfect divisors of the number 72.
When 72 is divided by any of the said numbers, it is divided completely and leaves zero as a remainder.
It can also be mentioned by using the methods of multiplication where two factors multiply perfectly to give the number 72.
Interestingly, 1 and the number itself (72) fall in the definition of factors for every number. So, 1 and 72 are also the factors of 72.
How To Calculate the Factors of 72?
To find the factors of 72, start dividing 72 by the smallest natural number that divides 72 perfectly and does not leave any remainder.
Continue dividing 72 by consecutive whole numbers, if the quotient is a whole number, it is a perfect divisor of 72. Hence, also it is a factor of 72.
If the quotient is a number in a fraction, it is not a factor of 72. Now let’s start the procedure:
Divide 72 by the smallest natural number i.e., 1.
\[\dfrac{72}{1} = 72 \]
As it has completely divided 72 without any leaving a remainder, so 1 is a factor of 72.
Now, divide 72 by the smallest even prime number i.e., 2
\[\dfrac{72}{2} = 36 \]
The number 72 has been divided perfectly by its divisor. So, the 2 is also a factor of 72.
Again divide 72 by the smallest odd prime number, which is 3
\[\dfrac{72}{3} = 24\]
As 3 has divided 72 completely. So, the number 3, too is a factor of 72.
For getting more factors, divided 72 by natural numbers that exactly divide 72 and leave zero remainders as shown below:
\[\dfrac{72}{4 }= 18 \]
\[\dfrac{72}{6} = 12 \]
\[\dfrac{72}{8} = 9 \]
\[\dfrac{72}{9} = 8 \]
\[\dfrac{72}{12} = 6 \]
\[\dfrac{72}{18} = 4 \]
\[\dfrac{72}{24} = 3 \]
\[\dfrac{72}{36} = 2 \]
\[\dfrac{72}{72} = 1 \]
All the above numbers completely divide 72 and do not leave any remainder. So, all these numbers are factors of 72.
The method stated above is called calculating the factors by division method. There are various methods to calculate the factors of 72. Other methods are also explained in this article.
Factors of 72 by Prime Factorization
The prime factorization of 72 is the expression of 72 as a product of its prime factors. To find out the factors of 72 by the prime factorization method, divide 72 by the smallest prime number which divides 72 exactly.
The resulted quotient is again divided by the smallest prime number and the procedure continues until we get 1 as the final quotient when cannot be divided any further.
Here are the steps to calculate factors of 72 by prime factorization.
The first step in the process is to divide 72 by the smallest prime number divisor which in this case is 2.
\[\dfrac{72}{2} = 36 \]
The quotient 36 is an even composite number and it further requires to be divided by 2 being the smallest available prime number divisor.
\[\dfrac{36}{2} = 18 \]
18 is again an even composite number that can be further divided by the prime number 2.
\[\dfrac{18}{2} = 9 \]
Now, as 9 cannot be completely divided by 2, we have to shift to the next smallest prime number that divides the quotient 9 completely and does not leave any remainder. In the given case, the next prime number is 3 which completely divides 9.
\[\dfrac{9}{3} = 3 \]
The quotient 3 now can only be further divided by 3 and thus give the next quotient as 1
\[\dfrac{3}{3} = 1 \]
The quotient 1 cannot be further divided.
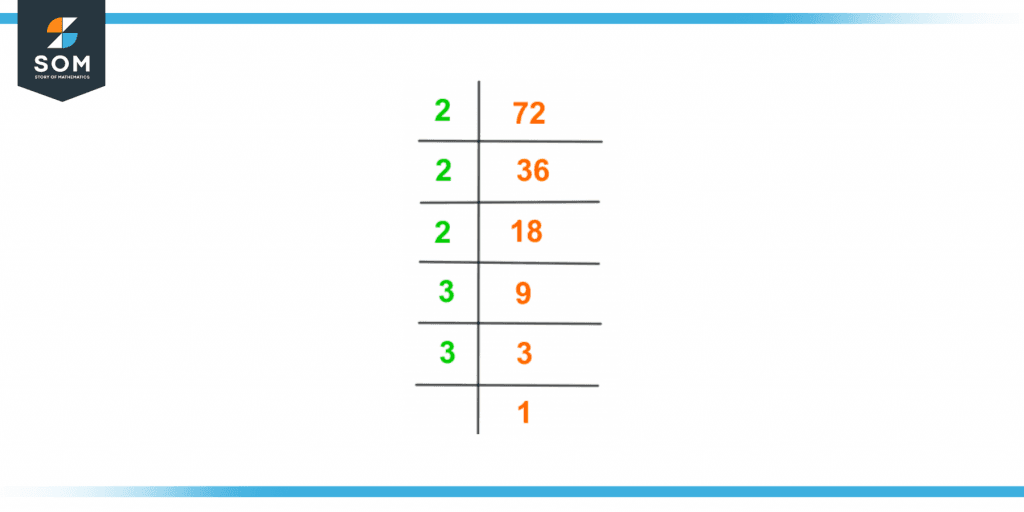
Figure 2 – Prime factorization of 72
Therefore, the prime factorization of 72 can be expressed as follows:
72 = 2 x 2 x 2 x 3 x 3
It can also be stated as:
72 = $2^3$ x $3^2$
Factor Tree of 72
Factors of 72 can also be expressed using a factor tree. It is a way of exhibiting the factors of a number, specifically the prime factorization of a number in which each branch of the tree divides into its factors.
These factors are distributed and written in the form of branches showing the given number’s factorization.
The splitting of a branch can either produce prime or composite numbers. If one of the branches resulting from a split, produces a composite number, the branching goes further. The method is continued until the factors at the end of the branch produce both the prime numbers. This is where the branching stops.
If we write 72 into multiples, it would be:
72 = 2 x 36
Upon dividing 36 into its multiples, it would be:
36 = 2 x 18
Dividing 18 further into its multiples would result in:
18 = 2 x 9
Further dividing 9 into its multiple factors would give:
9 = 3 x 3
By dividing 3 further into its multiples, it would be:
3 = 3 x 1
Expressing the number in terms of prime factors would give us:
2 x 2 x 2 x 3 x 3
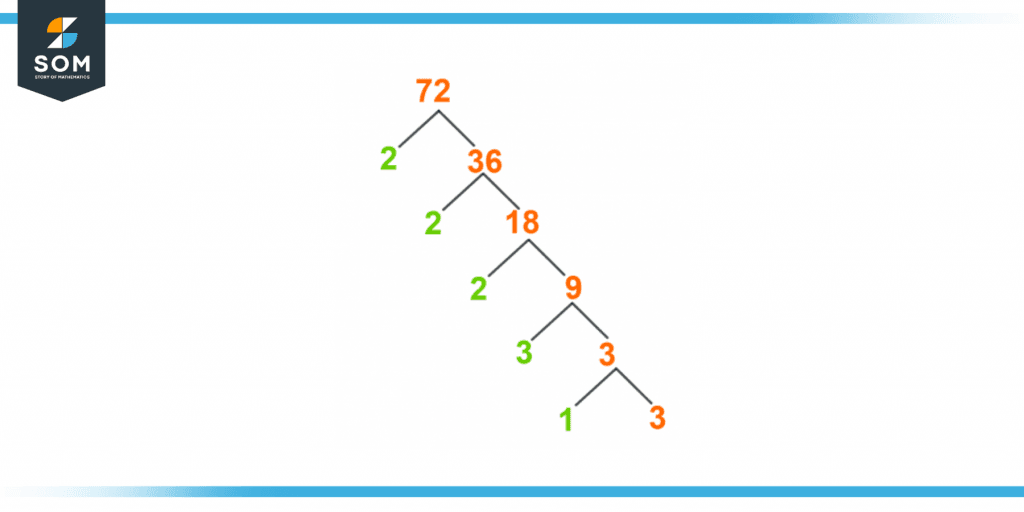
Figure 3 – Factor tree of 72
Factors of 72 in Pairs
Factor pairs of 72 are the two factors of 72 that, when multiplied together, give the product as 72. A set of two natural numbers whose product gives us the number 72 are called factors of 72 in pairs.
Pair Factors are a pair of numbers that, when multiplied by each other, give the result of 72 itself. Following are the pair factors of the number 72.
1 x 72 = 72
2 x 36 = 72
3 x 24 = 72
4 x 18 = 72
6 x 12 = 72
8 x 9 = 72
9 x 8 = 72
12 x 6 = 72
18 x 4 = 72
24 x 3 = 72
36 x 2 = 72
As there are 12 factors of 72, these factors can be written in pairs. The factors pairs of 72 are (1, 72), (2, 36), (3, 24), (4, 18), (6, 12), and (8, 9).
The number 72 can have negative pair factors, as well as the multiplication of two negative factors, also produces a positive product.
(-18) x (-4) = 72
(-6) x (-12) = 72
(-3) x (-24) = 72
Hence, here are some examples of negative pair factors of 72 such as (-1, -72), (-2, -36), (-3, -24), (-4, -18), (-6, -12), and (-8, -9).
So, it can be determined that the product of all factors of 72 in its negative form, gives the result 72. They are called negative pair factors of 72.
Tips and Tricks
- Every factor of a given number is either less than or equal to that given number but can never be greater than the number. Hence, the factor of 72 can never be greater than 72 itself.
- Only whole numbers and integers can be the factors of a given number.
- Any given number has only a finite number of factors/divisors as in this case, number 72 has only 12 factors.
- A trick to calculate the total number of factors of a given number can help calculate factors of large numbers and save some time. It can also be used to cross-check the conventional methods of calculating factors of a given number. For example, the prime factorizations of 72 are such as:
72 = $2^3$ x $3^2$
Add one (1) to the exponents which are 3 and 2 individually and multiply their sums. i.e.,
(3 +1) x (2 +1) = 12
This shows that 72 have 12 factors in total.
Factors of 72 Solved Examples
Example 1
What are the negative pair factors of 72?
Solution
Please keep in mind, that the product of two negative numbers is positive. So, all the factors of 72 in their negative form are called negative pair factors of 72. These are:
(-1, -72)
(-2, -36)
(-3, -24)
(-4, -18)
(-6, -12)
(-8, -9)
Example 2
Which of the following sentences is not true about factors of 72?
- 72 has a total of 12 factors.
- 72 has only two prime factors which are 2 and 3.
- 72 can have one positive and one negative factor in the pair.
- Pair Factors of 72 can have both one prime and one composite number.
Solution
The certain product of one positive and one negative number will always be negative. Hence, 72 can never have one positive and another negative factor in pairs. So False statement is 72 can have one positive and one negative factor in pairs.
Images/mathematical drawings are created with GeoGebra.
