JUMP TO TOPIC
Factors of 84: Prime Factorization, Methods, Tree, and Examples
Factors of 84 are all the numbers that we can evenly divide into 84. These numbers can be positive or negative. Factors do not produce any remainder. Note that dividing 84 with any factor of 84 will result in another factor of 84.

Figure 1 – All possible Factors of 84
Every possible number has a finite number of factors similarly 84 has a set of defined factors.
Let us dig in further to find out how to calculate the factors of 84, its factor tree, and the prime factorization along with examples.
What Are the Factors of 84?
Factors of 84 are the following: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, and 84. These numbers can divide 84 evenly or multiply together to form the number 84.
The number 84 has a total of 12 factors. Each of these factors gives a whole number as a result of dividing it by 84.
How To Calculate the Factors of 84?
In mathematics, we have 2 different ways to calculate the factors of any number, which are: Division Method and Multiplication Method.
In the Division method, we divide 84 by all numbers up to 84 to check which ones result in an evenly split quotient. When we do that, we can see that dividing 84 by these numbers resulted in an even quotient. So to find the factors we will follow these steps:
Start dividing the number 84 with the smallest integer. 1 is the smallest integer in the positive integer line. Since 1 is the factor of every number. This is because it is called a universal factor as it divides every number.
\[ \dfrac{84}{1}=84, remainder = 0\]
\[ \dfrac{84}{2}=42, remainder = 0\]
\[ \dfrac{84}{3}=28, remainder = 0\]
\[ \dfrac{84}{4}=21, remainder = 0\]
\[ \dfrac{84}{6}=14, remainder = 0\]
\[ \dfrac{84}{7}=12, remainder = 0\]
\[ \dfrac{84}{12}=7, remainder = 0\]
\[ \dfrac{84}{14}=6, remainder = 0\]
\[ \dfrac{84}{21}=4, remainder = 0\]
\[ \dfrac{84}{28}=3, remainder = 0\]
\[ \dfrac{84}{42}=2, remainder = 0\]
\[ \dfrac{84}{84}=1, remainder = 0\]
The above-given numbers qualify as the factors of 84 as they give zero remainders and a whole number quotient when divided by 84. Every number can have negative as well as positive factors just with the opposite signs.
If multiplying 2 numbers gives us 84 as the result, both the multiplier and multiplicand will be considered as the factors of that number. We can use this alternative method to calculate the factors of 84 in the following way:
1 x 84 = 84
2 x 42 = 84
3 x 28 = 84
4 x 21 = 84
6 x 14 = 84
7 x 12 = 84
Hence, the factors of 84 can be written as:
factors of 84 are 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
Similarly, we can also write the factors of 84 as multiplying the two negative values results in a positive value.
-1 x -84 = 84
-2 x -42 = 84
-3 x -28 = 84
-4 x -21 = 84
-6 x -14 = 84
-7 x -12 = 84
This gives us the same number of factors.
Negative factors of 84 = -1, -2, -3, -4, -6, -7, -12, -14, -21, -28, -42, -84
Factors of 84 by Prime Factorization
Prime factorization is one of the techniques used to find factors of numbers. The upside-down division is a method used in mathematics to find the prime factors of 84. Prime factors of 84 can be found using the following steps:
Firstly, start by dividing 84 with the smallest prime number, which is 2.
\[ \dfrac{84}{2}=42, remainder = 0\]
Since the answer is in whole numbers with a remainder of 0, we will continue dividing the answer until we get 1 as an answer.
\[ \dfrac{42}{2}=21, remainder = 0\]
21 is an odd number, we cannot divide it by 2. In this case, we will check the next prime number, which is 3.
\[ \dfrac{21}{3}=7, remainder = 0\]
The number 7 is not divisible by any number other than 1 and 7 itself, which means it’s a prime number.
\[ \dfrac{7}{7}=1\]
Remainder = 0
We have obtained 1 and can no longer continue the division. So the Prime Factorization of 84 can be written as:
2 x 2 x 3 x 7 = 84
The prime factorization of 84 is shown below in figure 2:
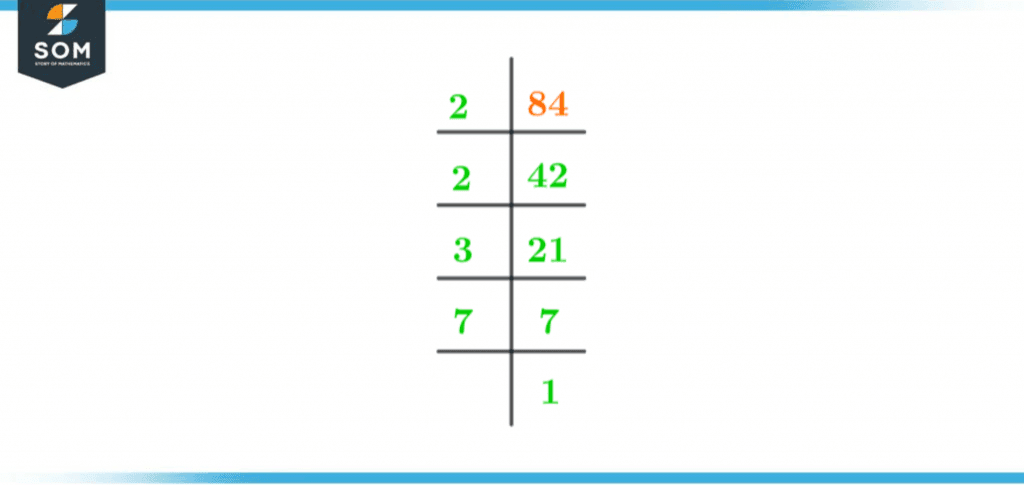
Figure 2 – Prime Factorization of 84
Factor Tree of 84
The factor tree of a number is a method to visually analyze all the Prime factors of that number. It acts like branches of a tree which logically help us understand the concepts of prime factorization.
It can also be defined as a pictorial description of the prime factorization of a particular number. The branches extend to produce one prime factor and one composite that can be further resolved into its prime factors. The tree continues till both the prime factors are obtained.
The factor tree of 84 is given below:
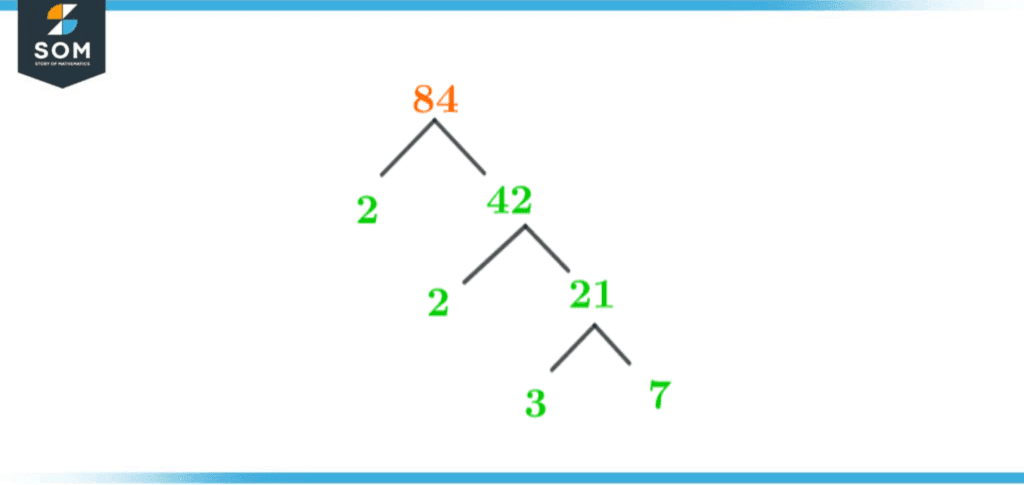
Figure 3 – Factor Tree of 84
Factors of 84 in Pairs
A Factor pair is the combination of two numbers that give us the required number i.e. 84 when multiplied by each other. The following are the factor pairs of the number 84:
1 x 84 = 84
2 x 42 = 84
3 x 28 = 84
4 x 21 = 84
6 x 14 = 84
7 x 12 = 84
The factor pairs of the number 84 are given as follows:
(1,84)
(2, 42)
(3, 28)
(4, 21)
(6, 14)
(7, 12).
We can also find the negative pair factors of 84 by using the same method.
-1 x -84 = 84
-2 x -42 = 84
-3 x -28 = 84
-4 x -21 = 84
-6 x -14 = 84
-7 x -12 = 84
Note that when we multiply two negative numbers, the answer will always be a positive number. Therefore the negative factor pairs are given as:
(-1,-84)
(-2, -42),
(-3, -28),
(-4, -21)
(-6, -14)
(-7, -12)
Factors of 84 Solved Examples
Example 1
It’s Emma’s 10th Birthday Party! Her Mom baked 40 tarts and 84 cookies for her friends. She wants to pack them in boxes in such a manner that each box has an equal number of tarts and cookies. What is the least number of boxes Emma’s mom would require for this?
Solution
To find the least number of boxes so that we can put tarts and cookies equally in the given boxes, let’s find the Greatest Common factors of 40 and 84.
As we know:
Factors of 40 are given as 1, 2, 4, 5, 8, 10, 20, 40
Similarly:
Factors of 84 are given as 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42 ,84
Therefore, the Common factors of 40 and 84 can be written as:
Common Factors = 1, 2, 4
So, the Greatest Common factor between 40 and 84 is:
Greatest Common factor = 4
Hence, at least 4 boxes are required.
Example 2
What are the positive and negative factor pairs of 84 and 86?
Solution
The negative factor pairs of a number are the same as the positive factor pairs just with the opposite signs.
The positive factor pairs of 84 are given as:
(1, 84)
(2, 42),
(3, 28),
(4, 21)
(6, 14)
(7, 12)
The negative factor pairs of 84 are given as:
(-1,-84)
(-2, -42),
(-3, -28),
(-4, -21)
(-6, -14)
(-7, -12)
The positive factor pairs of 86 are given as:
(1, 86)
(2, 43)
The negative factor pairs of 86 are given below:
(-1, -86)
(-2, -43)
Example 3
Find the LCM of 12 and 84.
Solution
For finding the LCM of 12 and 84, first, determine their prime factorization.
The prime factorization of 12 is given as:
12 = 2 x 2 x 3
The prime factorization of 84 is given as:
84 = 2 x 2 x 3 x 7
Therefore, the LCM of 12 and 84 is given as:
LCM = 2 x 2 x 3 x 7 = 84
Example 3
Find the LCM of 24 and 84. Also, determine the common factors.
Solution
a) To calculate the LCM of 24 and 84, first, determine the prime factorization of each 24 and 86.
The prime factorization of 24 is given as:
12 = 2 x 2 x 2 x 3
The prime factorization of 84 is given as:
84 = 2 x 2 x 3 x 7
Therefore, the LCM of 12 and 84 is given as:
LCM = 2 x 2 x 2 x 3 x 7 = 168
So, the LCM of 24 and 84 is 168.
b) The common factors of both the numbers 24 and 84 are given as:
Common Factors = 2 and 3
Images/mathematical drawings are created with GeoGebra.
