JUMP TO TOPIC
Factors of 87: Prime Factorization, Methods, Tree, and Examples
The factors of 87 are integers by which 87 is evenly divided. The remainder is also zero. When we multiply the divisor by the quotient, the product always equals the actual number.
Figure 1 – All possible Factors of 87
- Positive Factors
- Negative Factors
- Multiplication method
- Division method
What Are the Factors of 87?
The factors of 87 are 1, 3, 29, and 87. When we divide 87 by any of these factors, there will be no remainder after division. That means the remainder after is zero.There are a total of eight factors of 87. Four are positive factors, and the remaining four are negative ones.How To Calculate the Factors of 87?
You can calculate the factors of 87 by using various methods, and the two most common methods are the division and multiplication methods. We will discover both methods in this article.We must remember that a number’s factor can never be greater than the number itself. It might be equal, but it can’t be greater than the number.As we already know, 87 has more than two factors as it is a composite number. Factors of 87 by division method:Simple rules of division are followed. Any number that fulfills the requirements of being a factor is known as a factor of that specific number.Start the division with the smallest number. Divide 87 by 1:The number one is a factor of every integer because every number is completely divisible by 1.\[ \frac{87}{1} = 87 \]\[ \frac{87}{-1} = -87 \]Looking at the above division, we conclude that 1 and -1 are factors of 87.Divide 87 by 2:87 is not even, so it wouldn’t be divided by 2.\[ \frac{87}{2} = 43.5 \]The quotient is in decimal form, which means 2 is not a factor of 87.Divide 87 by 3:\[ \frac{87}{3} = 29 \]\[ \frac{87}{-3} = -29 \]When we divide 87 by 3, the number is evenly divided, and no remainder is left after division. Condition of factors is satisfied 3 and -3 are the factors of 87. Divide 87 by 5:\[ \frac{87}{5} = 17.4 \]Again. the remainder is a non-zero number, so 5 is not a factor of 87.Divide 87 by 29:\[ \frac{87}{29} = 3 \]\[ \frac{87}{-29} = -3 \]When we divide 87 by 29, the condition of factors is satisfied. The remainder is zero. As a result, 29 and -29 are the factor of 87.Divide 87 by 87:\[ \frac{87}{87} = 1 \]\[ \frac{87}{-87} = -1 \]When 87 is divided by itself. Condition of factors is satisfied. Every integer is a factor in itself. Every number divides itself evenly, and the remainder is always zero. 87 and -87 are the factors of 87.The positive factors list of 87 by division method: 1, 3, 29, 87. The negative factors list of 87 by division method: -1, -3, -28, -87. Factors of 87 by multiplication method:In this method, laws of multiplication are implemented. When we multiply the divisor by the quotient of the above divisions. The product is equal to the original number.1 x 87 = 87
-1 x -87 = 87
The product of two negative signs is always a positive whole number.3 x 29 = 87
-3 x -29 = 87
By the above multiplications, we can easily extract the factors list of 87.The positive factors list of 87 by multiplication method: 1, 3, 29, and 87.The negative factors list of 87 by multiplication method: -1, -3, -28, -87. If we compare the factors lists of both methods, we conclude that the factors will be the same. Whatever way you apply the basic concept should be clear.Factors of 87 by Prime Factorization
Prime factorization is a technique used to determine the prime factors of a number. It is a type of division that uses only prime factors of the given number. The division continues until 1 is received.In prime factorization, we figure out the prime factors of a given number that uniformly divide that number. In simple words, prime factorization is a way of expressing a number only by the product of its prime factors. The two most common methods of discovering prime factorizations are:- Division method
- Factor tree
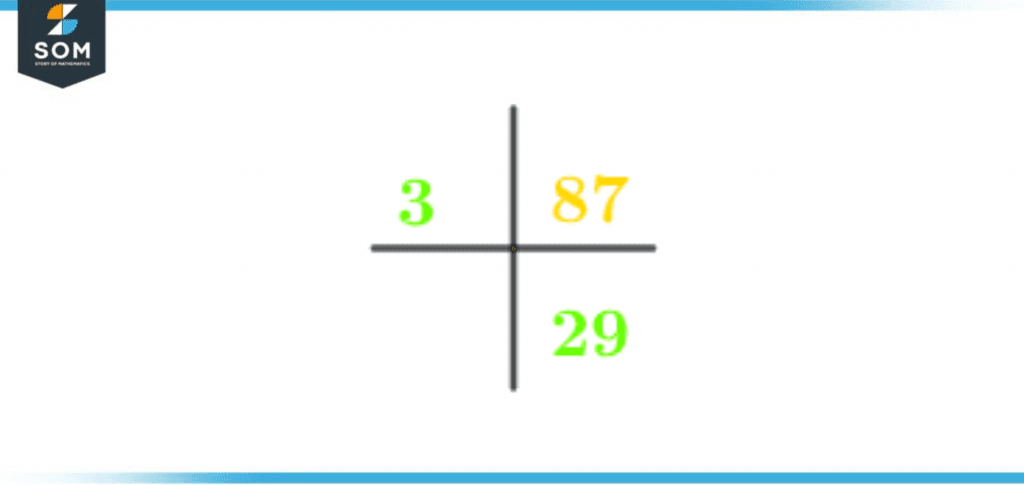
Figure 2 – Prime Factorization of 87
Prime Factorization of 87: 3 x 29
Factor Tree of 87
The factor tree is a pictorial representation of factors of any integer. Now we will learn how to construct a factor tree: The starting point of a factor tree is the given integer. That extends out into several branches. The ending point of a factor tree is where both branches have prime numbers. Write the number 87 at the top. Extend two branches out of it and fill them with the prime factors of 87 that divides it evenly.The factor tree of 87 is shown below in figure 3: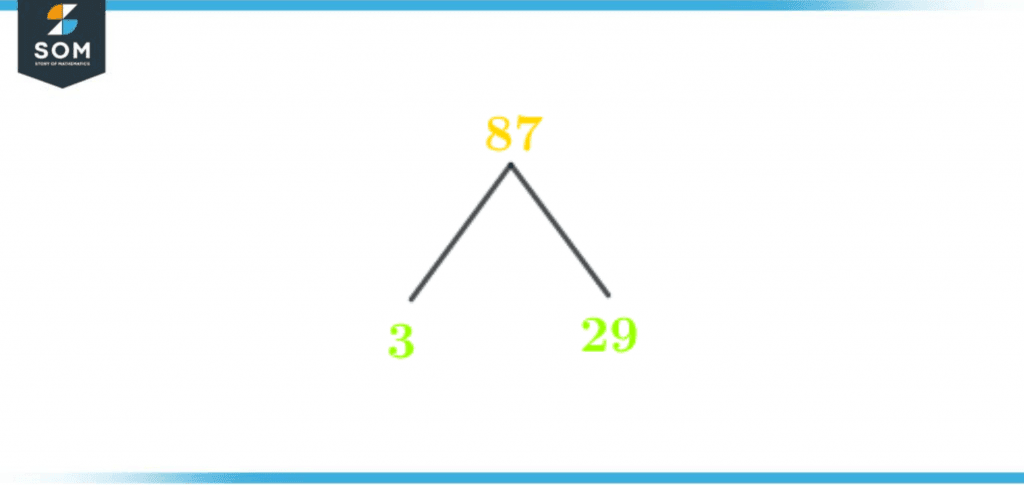
Figure 3 – Factor Tree of 87
Factors of 87 in Pairs
Factor pairs are sets of numbers that, when multiplied, give the original number as a product. The factor pairs can be both positive and negative, but they can’t be in fractional or decimal form.Finding factor pairs of 87 using the multiplication method:1 x 87 = 87
3 x 29 = 87
The positive factor pairs of 87 are the following:(1, 87)
(3, 29)
Now finding the negative factors of 87:-1 x -87 = 87
-3 x -29 = 87
The negative factor pairs of 87 are the following:(-1, -87)
(-3, -29)
Factors of 87 Solved Examples
For further enhancement of the concept, let’s solve some examples regarding factors of 87.Example 1
Help Zoe to find the average of aspects of 87.Solution
Firstly, find the factors of number 87:The factors list of 87: 1, 3, 29, 87
The average can be calculated by adding up all factors of 87 and dividing it by the total number of factors.Calculating the sum of all factors of 87:Sum: 1 + 3 + 29 + 87 = 120
Total number of factors of 87: 4Now divide the sum by the total number. \[ \frac{120}{4} = 30 \]Average = 30
Example 2
Find the sum of all prime factors of 87 and divide it by the sum of odd factors of 87.Solution
Factors of 87 = 1, 3, 29, 87.Finding the sum of all prime factors of 87Sum1: 3 + 29 = 32
Odd factors of 87: 1, 3, 29, 8787 is an odd number, and all its factors are odd. Finding the sum of all odd factors of 87Sum2: 1+ 3 + 29 + 87 = 120
Dividing sum1 by sum2: \[ \frac{120}{120} = 1 \]Example 3
Oliver wants to distribute 87 candies among 29 students. How much will each student get?Solution
Total number of students: 29Total number of candies: 87Divide the total number of candies by the total number of students. \[ \frac{87}{29} = 3 \]Each student will get three candies.
Images/mathematical drawings are created with GeoGebra.