JUMP TO TOPIC
Factors of 89: Prime Factorization, Methods, Tree, and Examples
Factors of 89 are the numbers that give off no remainder, and the final answer is always in integer/ whole number form. These are two necessities if the number has to be considered a factor.
Figure 1 – All possible Factors of 89
What Are the Factors of 89?
The factors of 89 are 1 and 89 as 89 is a prime number, which is why it has only two factors — 1 and the number itself. Though the number 89 is just a prime, you can still calculate its factors using both methods, multiplication or division. It is going to be shorter and more accessible for 89.How To Calculate the Factors of 89?
You can calculate a number’s factors by using the division or multiplication method. Calculating the factors of a specific number is a fundamental step and can be done perfectly if done carefully. Let’s take an overview of both processes.To find the factors of a number, you need to list down all the numbers that are either smaller than the number given or equal to it. Thus, the numbers will range from 44-89, among which the factors will be found by dividing them by 89.
Though there are innumerable ways to find out factors of a number, finding factors using multiplying and dividing are the easiest. Let’s look at an example of how you can find the factors of a number using the division method:
\[ \frac{89}{1} = 89 \]
\[ \frac{89}{2} = 44.5 \]
As can be seen above, when 89 is divided by one, the one answer we get is 89 (a whole number), whereas when we divide 89 by 2, the answer is in decimals. Thus, both 1 and 89 are considered the factors of this number. They also make a factor pair, i.e. (1, 89).
To find the factors of a number through division, you must start dividing the number, i.e., 89, by either the number equal to it or less than its half. When you get an answer in the whole number and the division gives off 0 remainders, the quotient and divisor of every such division are to be considered as the factors of 89. Let’s consider a few examples of how to find the factors of 89 using the division method: \[ \frac{89}{1} = 89 \]\[ \frac{89}{2} = 44 \]
\[ \frac{89}{3} = 29.66… \]
If we divide 89 by the numbers 2 and 3, our answer comes in decimals; thus, they cannot be considered factors of 89. However, as the division of 89 with one leaves no remainder and gives the answer in whole numbers, it is a factor of 89.
Once we reach the divisions until the number, it is an end to any further division.If you want to opt for the multiplication method, don’t worry. It is as easy as this one. When multiplied together, numbers that give 89 as the product will be considered as the factors of the specific number. Let’s take a look at a few examples:1 x 89 = 89
2 x 44 = 88
89 x 1 = 89
As written above, the multiplication of 2 with 44 gives 88 as the answer, whereas the rest two multiplications provide the number 89 as the answer; thus, 1 and 89 will be considered as the factors of 89. Therefore, there are only two factors of 89, which are 1 and 89, as it is a prime number.Factors of 89 by Prime Factorization
Prime Factorization is one of the easiest and most reliable ways to represent a number’s factors due to its prime factorization. Looking at the diagram, you can tell which prime factors multiply with each other to give the number, i.e., 89, as their product. Remember that 89 is a prime number and prime numbers only have two factors: one and the number; thus, representing prime factorization on diagrams for prime numbers is even easier! A diagram showing the Prime Factorization of 89 is attached below for a more precise concept: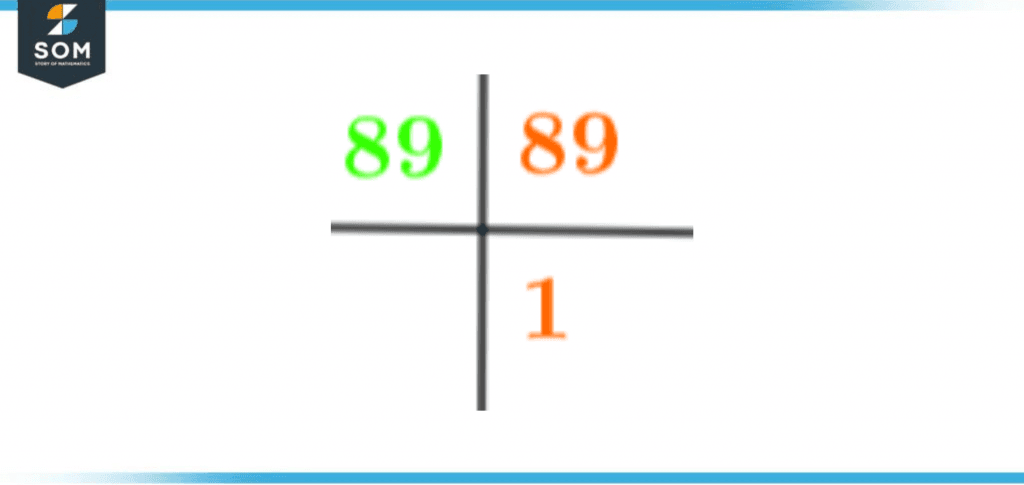
Figure 2 – Prime Factorization of 89
Factor Tree of 89
There isn’t just one easy way to represent the factors of a specific number. Making Factor Tree is one of the most used in many ways.By using this way of representing factors, you can graphically show and explain the factor chain of a number. The diagram is more like a tree with extended branches.The factor tree begins with the number itself, i.e., 89, and two branches represent the factors underneath. The factor tree continues till we reach the smallest prime number of the factors. Therefore, 1 and 89 are the only prime factors of 89 because 89 is a prime number.You can take a quick look at the diagram of the Factor Tree of 89 that is attached below: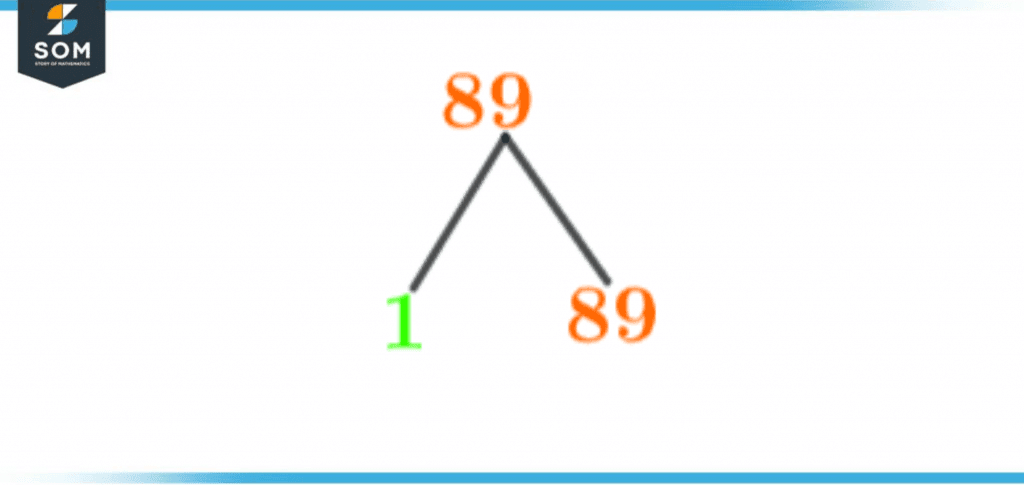
Figure 3 – Factor Tree of 89
- Very often in athletics, the best athlete is primarily the person who’s considered athlete number 89.
- 89 is the smallest prime number that has digits that are composites (8 and 9 both are composite numbers).
- 89 is the smallest number for which the positive sum of all odd primes less than or equal to it is a square
Factors of 89 in Pairs
Factor pairs are made when a number when a number is, e.g. divided by 89, and we get the answer in whole numbers, and no remainder is left; the quotient and divisor of such a division make a factor pair.As you know now that 89 is a prime number; thus, it only has 1-factor pair, i.e.:1 x 89 = 89, or it can also be written as:89 x 1 = 89.
The numbers 89 and 1 make up the only factor pair of this specific number.