Factors of 91: Prime Factorization, Methods, Tree, and Examples

Factors of 91 are defined as all the natural numbers that divide the number 91 entirely and leave no remainder behind. Factors of 91 can be rephrased as the two natural numbers that multiplied together in pairs to generate the number 91.

Figure 1 – All possible Factors of 91

This article explains all the necessary enlightenment needed to have a complete concept of the factors of 91 and the different techniques to find these factors. The customarily used methods to find factors of a number are the common division or multiplication method and the prime factorization method. 

Despite techniques used to find factors, this write-up explains the directions regarding the factor tree and factors in pairs with solved examples. 

What Are the Factors of 91?

The factors of 91 are 1, 7, 13, and 91.

91, being an odd and a composite number, has four factors. All the numbers are completely divisible by 91. The factors of 81 are the number that divides it wholly, with zero as the remainder.

Factors of 91 are also called divisors of 91. The divisors of 91 can be classified into proper divisors and improper divisors.

How To Calculate the Factors of 91?

The factors of 91 can be found via several methods: the division method, multiplication method, and prime factorization method.

Division

Here we will explain the calculation of factors by the standard division method. To find factors of 91 by this method, divide 91 by the smallest natural number, 1.

\[ \dfrac{91 }{1} = 91 , r = 0 \]

As one has perfectly divided the number 91 and left no remainder, 1 is a factor of 91.

Now consider the following consecutive natural number in the count, which is the smallest even prime number (2), to divide 91 into its factors.

\[ \frac{91}{ 2} = 45.5 \ (\text{Not a factor}) \]

It is clear that two does not divide the number 91 completely and produces a fraction in the quotient. Hence, 2 is not a factor of 91.

To find the rest of the factors of 91, continue dividing 91 by all the numbers in the list. The numbers that will produce zero remainders are regarded as factors:

\[ \dfrac{91}{7} = 13, r = 0 \]

\[\dfrac{91}{13} =7, r = 0 \]

Now, divide 91 by itself as below:

\[\dfrac{91}{91} = 1, r = 0\]

From the method mentioned above, the numbers which have wholly divided the number 91 without leaving any remainder behind are the factors of 91. The factors found through the above division method are 1, 7, 13, and 91.

Interesting Facts

For further understanding of the factors of 91, the following information must be recognized.

1. The most minor factor of 91 is 1.
2. The largest factor of 91 is the number 91 itself.
3. All the factors of 91 are odd numbers.
4. Except for 91, all the factors of 91 are prime numbers considering that 1 is not a prime nor a composite number.
5. The sum of divisors of 91 is an odd composite number 112.

Characteristics of the Number 91

Following are some essential characteristics of the number 91 which must be kept in mind to help understand and discover the factors of 91.

1. 91 is a  natural number that is an odd number simultaneously.
2. 91 is a composite number.
3. 91 is not a perfect square.
4. 91 is a semi-prime number.
5. 91 is not a defective number.

Factors of 91 by Prime Factorization

The prime factorization is the way of representing a given number in the form of the product of its prime factors. 

Differently, it can be defined as; the method of determining the factors of the given number. It utilizes the process of up-side-down division. The factors determined by prime factorization are prime factors.

The prime factorization has a base of division method, but the difference is that this method only uses prime numbers to divide the number 91.

Prime factors of the number are usually found by using the prime factorization technique. The below-described guidelines are followed to find out the factors of 91 by this method.

To start the process, firstly, determine the smallest prime number such that it is completely divisible without any remainder. The process continues with the number obtained. The number by which the division process starts is usually the smallest prime factor of the number.

This process continues until the final quotient one is achieved, which cannot be split further into its multiples.

The process is started by dividing the smallest prime factor by the given number 91, which in this case is 7

\[\dfrac{91}{7} = 13 \]

The resultant number (13) acquired from this division is a prime number and can be divided by itself only.

\[\dfrac{13}{13} = 1 \]

Here, the final result achieved 1, which cannot be divided any further, and the procedure stops here. The prime factorization of 91 can be expressed as:

Prime Factorization = 7 × 13

Prime factorization of 91 can also be expressed as:

91 = 7 x 13

The prime factorization of 91 is represented by the following figure 1.

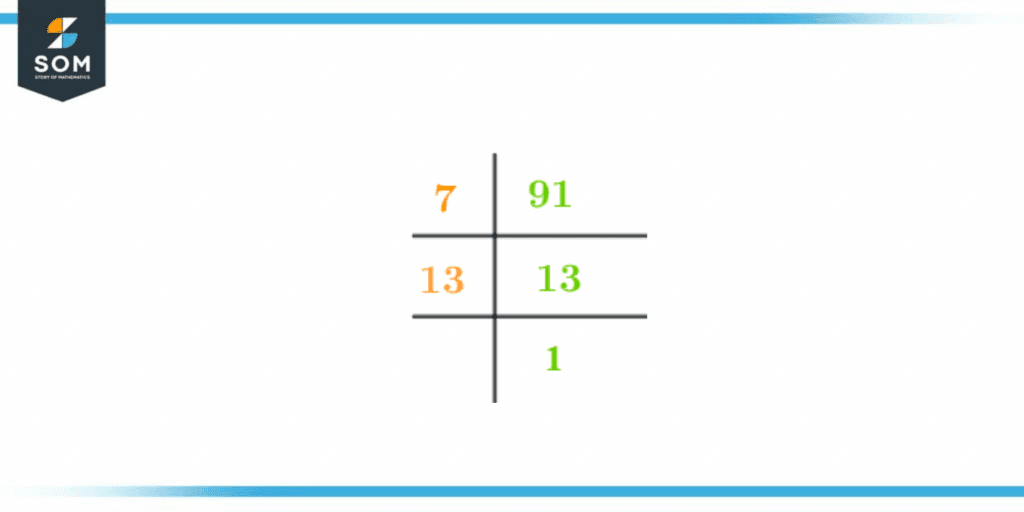
Figure 2 – Prime Factorization of 91

Factor Tree of 91

A factor tree is a separate way to find the factors of 91. The process utilizes the basic rules of prime factorization for this purpose, where the tree branching represents the division of the number under consideration.

The factor tree starts with the number 91 and continues to split into a prime number and a composite number. The factor tree is represented in the form of branches. The tree continues till further division is impossible.

The splitting of numbers terminates at the instant where a certain split produces prime numbers on both of its ends, and it can not be divided further.

For the given number, considering the rules of division by the factor tree method, If we write 91 into multiples, it would be;

 91 = 7 × 13

As the division has produced both the prime numbers in the first step. Hence, the procedure stops here after only the first divide.

The factors tree of 91 is represented in figure 2.

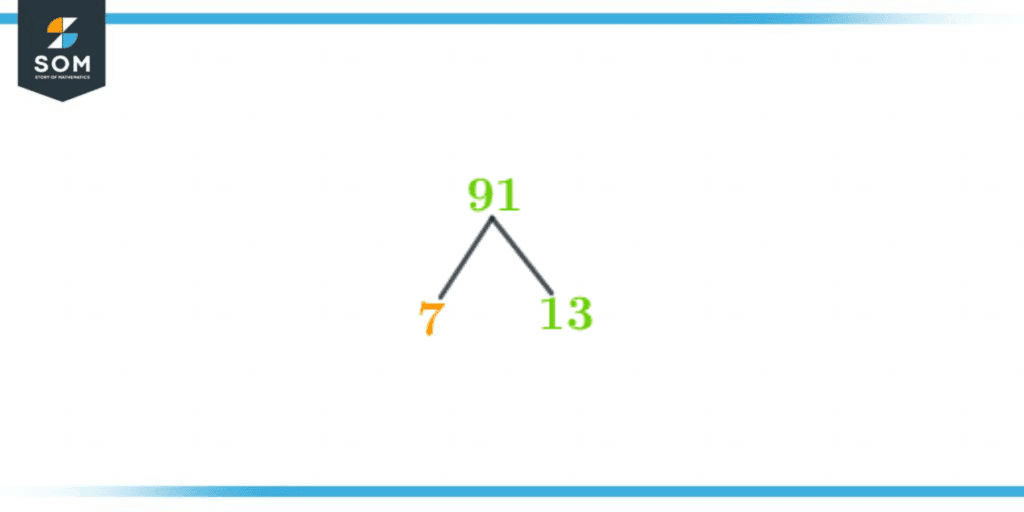
Figure 3 – Factor Tree of 91

Factors of 91 in Pairs

Factors of 91 in pairs are said to be the set of two integral numbers which multiply to produce the number 91.

The factor pair is the illustration of the product of the factors of the number 91 in the form of pair of numbers. The factor pairs show the factors of numbers in pairs yielding the number. The factor pairs can be determined as:

1 ×  91 = 91

7 ×  13 = 91

13 × 7 = 91

91 ×  1 = 91

The number 91 has only four factors in total which can be represented in sets of pairs as follows:

(1, 91)

(7, 13)

(13, 7)

(91, 1)

It is a universal fact that when a couple of negative numbers are multiplied together, they produce a positive integer. Hence additive inverse of all the factors of 91 can also be written in pairs. These are called negative pair factors of 91.

The following mathematical expressions can explain the negative pair factors of 91:

(-1) × (-91) = 91

(-7) × (-13) = 91

Therefore, the negative pair factors of number 91 are as follows:

(-1, -91)

(-7, -13)

Important Points

1. The factors of a number are divided by the number evenly.
2. Factors are neither decimals nor fractions.
3. Factors are positive and negative.
4. The factor pairs of number shows the factors in pairs.

Factors of 91 Solved Examples

Following are some solved examples related to the factors of 91.

Example 1

What is the prime factorization of 91?

Solution

The prime factorization of 91 can be shown as:

Prime Factorization of 91 = 7 × 13

Example 2

Find the sum of factors of 91.

Solution

The factors of 91 are 1, 7, 13, and 91.

Sum of factors of 91 = 1 + 7 + 13 + 91

Sum of factors of 91 = 112

Example 3

Anna was asked to segregate the prime and composite factors of 91. Please help Anna to do so.

Solution

Anna knows that the factors of 91 are 1, 7, 13, and 91.

Out of the four factors mentioned above, one is called the universal factor of 91, which is neither a prime nor a composite number.

The prime factors are 7 and 13, while the composite factor is only 91.

Images/mathematical drawings are created with GeoGebra