What Is 11/27 as a Decimal + Solution With Free Steps
The fraction 11/27 as a decimal is equal to 0.407.
Fractions are a more convenient way of representing the division of two numbers p and q. Instead of p $\boldsymbol\div$ q, fractions have the form p/q, where the dividend p is the numerator and the divisor q is the denominator. There are several types of fractions, and 11/27 is a proper fraction.
Here, we are more interested in the division types that result in a Decimal value, as this can be expressed as a Fraction. We see fractions as a way of showing two numbers having the operation of Division between them that result in a value that lies between two Integers.

Now, we introduce the method used to solve said fraction to decimal conversion, called Long Division, which we will discuss in detail moving forward. So, let’s go through the Solution of fraction 11/27.
Solution
First, we convert the fraction components, i.e., the numerator and the denominator, and transform them into the division constituents, i.e., the Dividend and the Divisor, respectively.
This can be done as follows:
Dividend = 11
Divisor = 27
Now, we introduce the most important quantity in our division process: the Quotient. The value represents the Solution to our division and can be expressed as having the following relationship with the Division constituents:
Quotient = Dividend $\div$ Divisor = 11 $\div$ 27
This is when we go through the Long Division solution to our problem.
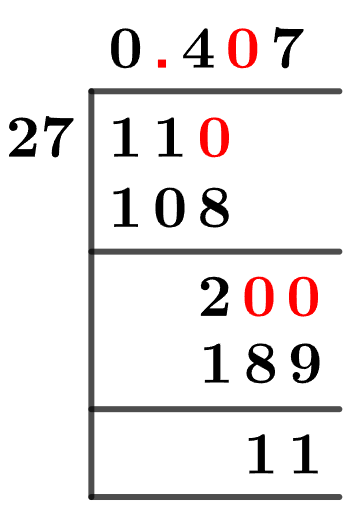
Figure 1
11/27 Long Division Method
We start solving a problem using the Long Division Method by first taking apart the division’s components and comparing them. As we have 11 and 27, we can see how 11 is Smaller than 27, and to solve this division, we require that 11 be Bigger than 27.
This is done by multiplying the dividend by 10 and checking whether it is bigger than the divisor or not. If so, we calculate the Multiple of the divisor closest to the dividend and subtract it from the Dividend. This produces the Remainder, which we then use as the dividend later.
Now, we begin solving for our dividend 11, which after getting multiplied by 10 becomes 110.
We take this 110 and divide it by 27; this can be done as follows:
110 $\div$ 27 $\approx$ 4
Where:
27 x 4 = 108
We add 4 to our quotient. This will lead to the generation of a Remainder equal to 110 – 108 = 2. Now this means we have to repeat the process by Converting the 2 into 200.
This needs a double multiplication of 2 by 10 as 2 x 10 = 20 which is smaller than 27. For this step, the quotient will be zero with a remainder of 20. So, we take a shortcut and add 0 to our quotient directly. Solving for 200 now:
200 $\div$ 27 $\approx$ 7
Where:
27 x 7 = 189
We add 7 to our quotient. This, therefore, produces another Remainder which is equal to 200 – 189 = 11. As we have the three decimal places now, we get the Quotient as 0.407 with a final remainder of 11.

Images/mathematical drawings are created with GeoGebra.
