What Is 17/20 as a Decimal + Solution With Free Steps

The fraction 17/20 as a decimal is equal to 0.85.The term Fraction refers to a mathematical expression that tells us how many equal portions combine to make up a given object.It has a unique representation in which its two components numerator and denominator are divided by a line. The component appearing above the line is known as the Numerator, while that appearing below the line is known as the Denominator.For example, in the given fraction of 17/20, 17 is the numerator and 20 is the denominator.Such fractions can be solved easily by the method of Long Division, which is explained below in detail.

Solution

We usually solve fractions by division, which has two components, the dividend, and the divisor. The number which we have to divide is known as a Dividend, while the number that is dividing is known as Divisor. It tells us how many pieces we have to divide the dividend.The mathematical representation of the given fraction is:

Dividend = 17

Divisor = 20 

It means that we want to divide 17 into 20 equal parts. We get the magnitude of 1 part in the result, termed the Quotient.

Quotient = Dividend $\div$ Divisor = 17 $\div$ 20

Sometimes we are unable to fully divide a fraction and some quantity is left behind. This left-over quantity is known as Remainder.The Long Division approach is usually used to solve a fraction. Its complete steps are shown below.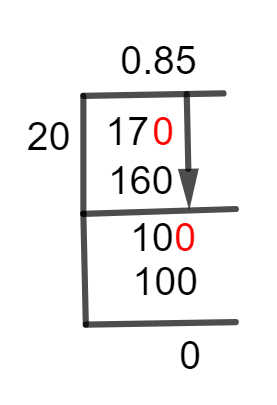

Figure 1

17/20 Long Division Method

The fraction given to solve is:

 17 $\div$ 20 

In a fraction, if the divisor or denominator is of greater numerical value than the numerator or dividend, it is known as a Proper Fraction. Such fraction has less than 1 decimal value. To solve such a fraction, we have to introduce a Decimal Point in our final result, which is the quotient. We can do this by multiplying the dividend by 10.As we know, our example 17/20 is a proper fraction. Because 20 is a bigger number as compared to 17, to calculate our result, we multiply 17 by 10 and introduce a decimal point in our quotient. Now, 170 is divided by 20 as:170 $\div$ 20 $\approx$ 8\]Where:

20 x 8 = 160

When we subtract 160 from 170, we get a remainder of 10 as shown below:

170 – 160 = 10

Since we get a non-zero remainder, so to calculate the accurate value of the quotient, we multiply it by 10 and get 100 to be divided by 20.

100 $\div$ 20 $\approx$ 5

Where:

20 x 5 = 100 

The remainder is determined as:

100 – 100 = 0

So we have a zero Remainder now. This illustrates that the fraction is fully solved 0.85 is the Decimal Value of 17/20. Also, it shows that 20 and 0.85 are factors of 17.Images/mathematical drawings are created with GeoGebra.