What Is 2 3/8 as a Decimal + Solution With Free Steps
The fraction 2 3/8 as a decimal is equal to 2.375.
Fundamentally, a fraction is the ratio of two whole numbers, which are separated by the dividing line. The numerator is the term for the number above the line, and the denominator is the number below the line. Proper fractions, improper fractions, and mixed fractions are the three forms of fractions that are most common.
Proper fractions are the numbers in which the numerator is less than the denominator, whereas improper fractions are the numbers in which the numerator is more than the denominator. A mixed fraction is produced when a whole number and an improper fraction are combined.
We utilize a technique known as the Long Division method to solve a fraction and obtain the result in decimal values. We can convert a mixed fraction of 2 3/8 to a decimal value by using the long division technique.
Solution
We must first turn this mixed fraction into an improper fraction before we can begin to solve the problem. The denominator 8 is multiplied by the whole number 2 and the result is then added to the numerator. As a result, the fraction we now have is 19/8.
The Dividend and the Divisor are two terms that are necessary to understand. The numerator and denominator are referred to as the dividend and the divisor, respectively.
Dividend = 19
Divisor = 8
Now, by introducing a new term called Quotient, which is defined as the outcome of the intended division.
Quotient = Dividend $\div$ Divisor = 19 $\div$ 8
Using the long division method, the problem can now be resolved as follows: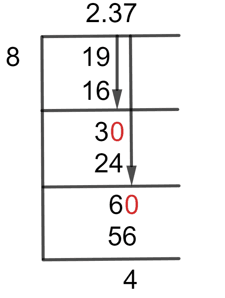
Figure 1
19/8 Long Division Method
This is how to use the long division method to solve the fraction step-by-step.
The fraction we had:
19 $\div$ 8
We can divide both terms directly because the numerator 19 is greater than the denominator 8.
Another division-specific term is used in the long division method, which is known as the Remainder. It is the remaining number after the division.
19 $\div$ 8 $\approx$ 2
Where:
8 x 2 = 16
After this step, the Remainder we have is 3.
The Decimal point must now be added because the remainder is now smaller than the divisor. We can proceed with our solution by adding a decimal point to the quotient and then adding a zero to the right of the remainder.
So by doing this, the remainder we have is 30.
30 $\div$ 8 $\approx$ 3
Where:
8 x 3 = 24
This results in the Remainder being equal to 6. As adding another zero to its right will result in 60, we must determine the following to solve to three decimal places:
60 $\div$ 8 $\approx$ 7
Where:
8 x 7 = 56
For the fraction 2 3/8, the Quotient is 2.37 with a Remainder of 4.
Images/mathematical drawings are created with GeoGebra.
