What Is 2/49 as a Decimal + Solution With Free Steps
The fraction 2/49 as a decimal is equal to 0.0408.
Mainly three different ways are used for the representation of rational numbers. They are a fraction, a percentage, or as decimals. Fractional representation is the most widely used. The fraction 2/49 is a proper fraction.

Here, we are more interested in the division types that result in a Decimal value, as this can be expressed as a Fraction. We see fractions as a way of showing two numbers having the operation of Division between them that result in a value that lies between two Integers.
Now, we introduce the method used to solve said fraction to decimal conversion, called Long Division, which we will discuss in detail moving forward. So, let’s go through the Solution of fraction 2/49.
Solution
First, we convert the fraction components, i.e., the numerator and the denominator, and transform them into the division constituents, i.e., the Dividend and the Divisor, respectively.
This can be done as follows:
Dividend = 2
Divisor = 49
Now, we introduce the most important quantity in our division process: the Quotient. The value represents the Solution to our division and can be expressed as having the following relationship with the Division constituents:
Quotient = Dividend $\div$ Divisor = 2 $\div$ 49
This is when we go through the Long Division solution to our problem. The following figure shows the solution for fraction 2/49.
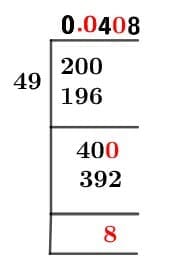
Figure 1
2/49 Long Division Method
We start solving a problem using the Long Division Method by first taking apart the division’s components and comparing them. As we have 2 and 49, we can see how 2 is Smaller than 49, and to solve this division, we require that 2 be Bigger than 49.
This is done by multiplying the dividend by 10 and checking whether it is bigger than the divisor or not. If so, we calculate the Multiple of the divisor closest to the dividend and subtract it from the Dividend. This produces the Remainder, which we then use as the dividend later.
After multiplying the dividend 2 by 10, we get 20 which is smaller than 49. That means division is not possible. So to make it bigger than 49, the 20 is again multiplied by 10 which gives us 200. This is done by putting a zero in the quotient after the decimal point.
Now, we begin solving for our dividend 200.
200 $\div$ 49 $\approx$ 4
Where:
49 x 4 = 196
This will lead to the generation of a Remainder equal to 200 – 196 = 4. After multiplying 4 by 10, we get 40 which is smaller than 49. That means division is not possible. So to make it bigger than 49, the 40 is again multiplied by 10 which gives us 400.
This is done by putting a zero in the quotient after the decimal point.
400 $\div$ 49 $\approx$ 8
Where:
49 x 8 = 392
Finally, we have a Quotient generated after combining the four pieces of it as 0.0408, with a Remainder equal to 8.
Images/mathematical drawings are created with GeoGebra.
