What Is 3 3/4 as a Decimal + Solution With Free Steps

The fraction 3 3/4 as a decimal is equal to 3.75.
When a proper fraction and a whole number are expressed together, a Mixed Fraction is formed. For instance, combining a whole number 3 with a proper fraction of 3/4 results in the mixed fraction 3 3/4.
Most of the time, fractions are used in mathematical operations after converting them into decimals because decimal values are simpler to work with within these computations compared to fractions. Different methods can be used for this conversion, one of which is Long Division.
Here, the Long Division method is discussed in detail for the conversion of 3 ¾ into a decimal.
Solution
Getting an improper fraction from a mixed fraction is the first step toward its solution. To do this, we must first calculate the product of the denominator and the whole number, and then we add it to the numerator.
The outcome will be the numerator of the improper fraction. In the example of 3 3/4, we first calculate the product of 3 and 4 and then add it to 3. The outcome is 15, which is the numerator of the improper fraction. But the denominator of the improper fraction will be equal to the denominator of the mixed fraction.
Hence, we get an improper fraction of 15/4. For simplification, this fraction should be converted into division, by classifying its constituents or elements based on their functions. After doing this, we found 15 to be the Dividend and 4 to be the Divisor.
Dividend = 15
Divisor = 4
After the complete division of these two numbers, we get our result as a decimal number, which is known as Quotient.
Quotient = Dividend $\div$ Divisor = 15 $\div$ 4
In some cases, it is impossible to divide two numbers completely and have some leftover amount or value, known as the Remainder.
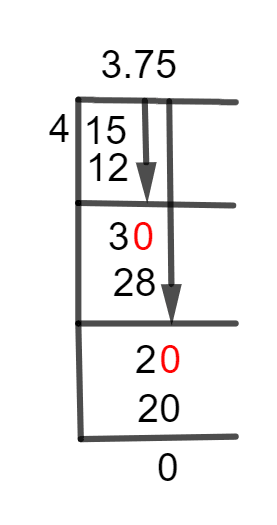
Figure 1
3 3/4 Long Division Method
3 3/4 is written in the form of an improper fraction as:
15 $\div$ 4
15 is divided by 4 as:
15 $\div$ 4 $\approx$ 3
Where:
4 x 3 = 12
Since 4 is not a factor of 15, so we are left with a remaining value of 3.
15 – 12 =3
To completely divide the fraction 15/4, we will require a decimal point. For this, we will add a zero to the right of our remainder, which is 3, and get 30. The division of 30 by 4 is shown below.
30 $\div$ 4 $\approx$ 7
Where:
4 x 7 = 28
This time we have 2 as a remaining value.
30 –28 =2
This 2 becomes 20 by the insertion of a zero to its right, which is then divided by 4.
20 $\div$4 4 $\approx$ 5
Where:
4 x 5 = 20
Now, we get no remaining value.
20 –20 =0
Thus, the decimal value of 3 3/4 is 3.75.
Images/mathematical drawings are created with GeoGebra.
3/6 As A Decimal | Fractions to Decimals List | 7/25 As A Decimal
