What is a 3 3/8 as a Decimal + Solution With Free Steps
The fraction 3 3/8 as a decimal is equivalent to 3.375.
Fractions are classified into three categories: mixed fraction, proper fraction, and improper fraction. For the conversion of any specified fraction into a decimal, it is necessary to first identify the type of the fraction.
A fraction is said to be improper when its numerator is is either equal to or greater than the denominator. Similarly, a fraction is said to be a proper function when the numerator is less than the denominator.
Mixed fractions, on the other hand, are a combination of a whole number and a proper fraction. The fraction 3 3/8 is considered a mixed fraction because it consists of the whole number 3 along with a proper fraction 3/8.
Now that we have identified our fraction, let’s dive into its detailed solution through the Long Division Method.
Solution
The given fraction 3 3/8 is a mixed fraction, so before proceeding toward the solution, it is first necessary to convert this mixed fraction into an improper fraction. For this purpose, firstly multiply the denominator 8 with the whole number 3.
Upon multiplying the 3 and 8, the result obtained is 24. Now add this number to the numerator to obtain an improper fraction. Hence, the improper fraction obtained after solving the mixed fraction is 27/8.
Before diving into the detailed solution, let’s take a look at some basic division terminology. For long division, the denominator of the fraction is referred to as the “Divisor” and the numerator is referred to as the “Dividend”. The result obtained is called “Quotient.” he
Dividend = 27
Divisor = 8
This division can be represented as follows:
Dividend $\div$ Divisor = Quotient
Another term used in the division is known as the “Remainder” and it is the number that is left when the division process comes to an end.
The long division process for 27/8 is shown below:
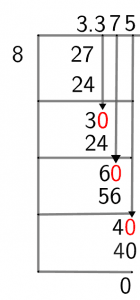
Figure 1
3 3/8 by Long Division
The long division method is used to convert 3 3/8 into a decimal form. Before moving onto the division, 3 3/8 is reduced to an improper fraction, 27/8. Now, we will carry the division of 27/8.
27 $\div$ 8
Since the dividend is greater than the divisor, so the two numbers can be divided.
27 $\div$ 8 $\approx$ 3
Where:
3 x 8 = 24
So after the first division step, a remainder of 3 is obtained. Now 3 will act as the dividend and since 3 is less than the divisor, so we will add a decimal point to insert an additional zero into the dividend. This converts 3 into 30.
30 $\div$ 8 $\approx$ 3
Where:
3 x 8 = 24
So, 6 is obtained as the remainder. Adding an additional zero into the dividend:
60 $\div$ 8 $\approx$ 7
Where:
8 x 7 = 56
Now, a remainder of 4 is obtained. Again adding a zero into the dividend:
40 $\div$ 8 = 5
This produces a remainder of zero, which marks the end of the division process. Thus, the quotient of 3 3/8 is 3.375.
Images/mathematical drawings are created with GeoGebra.
