What Is 3/7 as a Decimal + Solution With Free Steps
The fraction 3/7 as a decimal is equal to 0.428.An expression in mathematics that demonstrates how many parts a number can be divided into is known as a Fraction. Its constituents include a numerator and a denominator separated by a line. The Numerator is the number present above the line, whereas the Denominator is a number below the line.Here, we will explain the Long Division method to solve a fraction.Solution
To solve a fraction, we have to start by transforming it into division. Since components of the division include Dividend and Divisor, so the numerator of the fraction becomes dividend and the denominator becomes divisor. In the example to solve, we get 3 as a dividend and 7 as a divisor. This can be mathematically represented as:Dividend = 3
Divisor = 7
Fraction of 3/7 means the division of 3 into 7 equal parts. When solving this fraction we get the magnitude of 1 part as the Quotient, which is known as the final result of division. However, if a fraction is not fully divided, we get some quantity left behind. This is known as Remainder.Quotient = Dividend $\div$ Divisor = 3 $\div$7
The given fraction of 3/7 is solved using Long Division and the solution is presented below: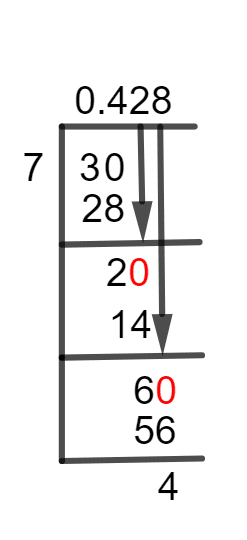
Figure 1
3/7 Long Division Method
Below is a step-by-step explanation to solve the given fraction. We have:3 $\div$ 7
While solving a division sum or fraction, the first step is to find, whether it is a Proper or an Improper Fraction. In the given fraction, we have 3 as a dividend, which is smaller than 7, the divisor. So this is a proper fraction. Hence, we have a requirement of a Decimal Point to complete our calculations. We can do this by adding a zero to the right of our dividend. By doing this, we get 30, which will now be divided by 7.30 $\div$ 7 $\approx$ 4
Where:7 x 4 = 28
The remainder is 30 – 28 = 2, which is greater than zero. So, we again add a zero to its right but without any decimal point and make it 20. Further calculations are presented as:20 $\div$ 7 $\approx$ 2
Where:7 x 2 = 14
This time the remainder is 20 – 14 = 6. Again 6 is smaller than 7, so we make it 60 by inserting a zero to its right. Now, 60 is divided by 7.60 $\div$ 7 $\approx$ 8
Where:7 x 8 = 56
Now, the remainder is:60 – 56 = 4
Again, there is a non-zero remainder produced. This shows that the fraction is partially divided and we get a Quotient of 0.428 with a Remainder equal to 4. We solve it up to more decimal places to get a more accurate answer.
Images/mathematical drawings are created with GeoGebra.