What Is 3/8 as a Decimal + Solution With Free Steps
The fraction 3/8 as a decimal is equal to 0.375.The division is one of four fundamental operations of mathematics. It is the process of splitting something up into pieces or being split up. The division is the inverse of multiplication. In the given problem, Long Division is used to solve a fraction of 3/8.Solution
To solve a given fraction first, the fraction components are separated according to their function. When dividing a fraction, the numerator is referred to as the Dividend and the denominator as the Divisor. Here dividend is 3 and the divisor is 8. Thus, the fraction given in the question is represented as:Dividend = 3
Divisor = 8
After completing the process of division, Quotient is used to represent its result, while Remainder is the remaining value that is obtained as a result of incomplete division.Quotient = Dividend $\div$ Divisor = 3 $\div$ 8
Now, this fraction can be solved by using the method of Long Division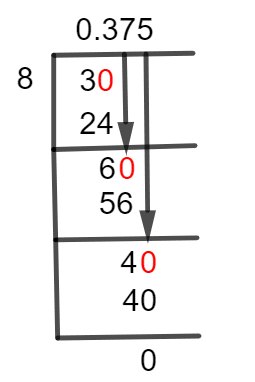
Figure 1
3/8 Long Division Method
Long division is a technique for the division of large numbers that divides the task into several sequential phases. Similar to conventional division problems, the dividend is divided by the divisor to get the quotient, and occasionally it also produces a remainder.The method of Long Division to solve a given fraction can be understood as follows.We had:3 $\div$ 8
In long division, we check if the first digit of the dividend is greater than the divisor. As in the given example, dividend 3 is less than divisor 8, so we need a Decimal Point to solve this fraction. For this purpose, we insert a zero to the right of the remainder.In this case, Remainder 3 becomes 30 after inserting a zero to its right. Now, we divide 30 by 8, which gives us the following result.30 $\div$ 8 $\approx$ 3
Where:8 x 3 = 24
It shows that a Remainder is produced due to this division, which is equal to 6.30 – 24 = 6
Since a remainder is produced, so we again insert a zero to the right of the remainder but without using the Decimal point because Quotient already has a decimal value.The resulting value of the remainder of 6 will become 60 after plugging in a zero to its right. Now, the next step can be computed as:60 $\div$ 8 $\approx$ 7
Where:8 x 7 = 56
This time we have 4 as a Remainder. Insertion of another zero will give us 40. The further calculation can be carried out as follows.40 $\div$ 8 $\approx$ 5
Where:8 x 5 = 40
Now, the Quotient is 0.375 and the Remainder is 0. This indicates that this is the accurate result of this division and there is no need to solve it further.
Images/mathematical drawings are created with GeoGebra.