What Is 5/16 as a Decimal + Solution With Free Steps
 The fraction 5/16 as a decimal is equal to 0.3125.
The fraction 5/16 as a decimal is equal to 0.3125.
Fractions are represented in p/q, where p is the numerator and q shows the denominator. The numerator and denominator are separated by the line, which is the division symbol.
Division seems like a difficult one among all the mathematical operations, but actually, it is not that tough because there is a solution to deal with this tough problem. The Long Division method can be used to deal with such challenging problems.
Here is the complete solution to solve the given fraction, i.e., 5/16, that will produce the decimal equivalent using the method called Long Division.
Solution
First, it is important to separate the constituents of the fraction depending on the nature of their operation. When we have a fraction in p/q, the numerator is called the dividend and the denominator is known as divisor.
Dividend = 5
Divisor = 16
When we solve a fraction-based problem by the long division method, the result of the fraction in decimal form is referred to as the Quotient.
Quotient = Dividend $\div$ Divisor = 5 $\div$ 16
Now, by using the Long Division, we can solve the problem as: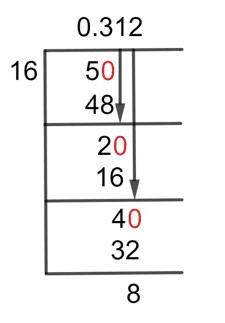
Figure 1
5/16 Long Division Method
By having a closer look at the Long Division method, the solution is seen below.
The fraction we had:
5 $\div$ 16
As it can be seen that the denominator of 16 is greater than the numerator, which means we have to add the decimal point to the quotient first. So, by adding a decimal point, we can now multiply our dividend with 10 to proceed to our solution using the long division method.
There is a need for another term to be introduced here, which is the remaining part after the division and is referred to as the Remainder.
So here the remainder is 5, so we first add the Decimal point to the Quotient and then add the Zero to the Remainder’s right to start our first step of the method:
50 $\div$ 16 $\approx$ 3
Where:
16 x 3 = 48
This indicates that a Remainder was also generated from this division, and it is equal to 50 – 48 = 2.
So the remainder we have now from the previous step is 2, so adding zero to its right will make it 20, and this time there is no need to add the decimal point as it is already in the quotient.
20 $\div$ 16 $\approx$ 1
Where:
16 x 1 = 16
So, after this, the Remainder is equal to 4. By bringing in another zero to its right, it becomes 40, so by solving this we get an answer in three decimal places:
40 $\div$ 16 $\approx$ 2
Where:
16 x 2 = 32
Now the remainder is 8, with a resulting Quotient of 0.312.
Images/mathematical drawings are created with GeoGebra.
