What Is 5 3/4 as a Decimal + Solution With Free Steps
The fraction 5 3/4 as a decimal is equal to 5.75.
Mixed fraction is the name given to the provided fraction. A mixed fraction is any fraction that contains both a whole number and an improper fraction. The three main categories of fractions are improper fractions, proper fractions, and mixed fractions.
It’s called an improper fraction when the fraction’s numerator is higher than its denominator. Similarly, a fraction with a denominator smaller than the numerator is known as a proper fraction.
In this case, we must change the mixed fraction of 5 3/4 into a decimal value. We must divide a fraction to get its decimal equivalent. In mathematics questions, the division also appears to be one of the trickiest operations, but there is a solution. Long Division is the technique we employ to resolve the fraction.
Solution
We will first change the given mixed fraction into an improper fraction. To do it, multiply the whole number by the denominator, then add the numerator to the result. Therefore, 23/4 is the corresponding mixed fraction of 5 3/4.
Before beginning the solution, it is necessary to introduce the terms “Dividend” and “Divisor,” which are terms specific to dividends. The fraction’s numerator is the dividend, and its denominator is the divisor.
Dividend = 23
Divisor = 4
Here, we will introduce a new word, the Quotient, which is essentially the result of the fraction in decimal form.
Quotient = Dividend $ \div $ Divisor = 23 $ \div $ 4
The following is the long division method’s answer: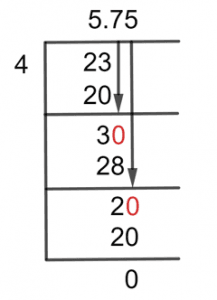
Figure 1
23/4 Long Division Method
By using the long division method, we may solve the fraction step-by-step as follows:
23 $ \div $ 4
We can divide the two values directly because the numerator is greater than the denominator.
Let’s introduce a new word right now. The Remainder is the number left behind when two numbers are not perfectly divisible by one another.
23 $ \div $ 4 $ \approx $ 5
Where:
4 x 5 = 20
We have a remainder of 3.
Now that we have a remainder that is less than the divisor, we must multiply it by ten. To do that, we shall add the decimal point to the quotient’s value.
So now we have a remainder of 30.
30 $ \div $ 4 $ \approx $ 28
Where:
4 x 7 = 28
So now we have a remainder of 2. Again, we will multiply our remainder by ten to further progress our solution as we did in the previous step, but here there will not be a decimal point in the quotient because we already did that in the previous step.
20 $ \div $ 4 $ = 5
Where:
4 x 5 = 20
As a result, the provided mixed fraction of 5 3/4 has a Quotient of 5.75 with the remainder being 0, which is obtained by using the Long Division method.
Images/mathematical drawings are created with GeoGebra.
