What Is 7/2 as a Decimal + Solution With Free Steps

The fraction 7/2 as a decimal is equal to 3.5.
The total number of equally sized pieces combined to form a whole thing or object. It is expressed mathematically as a Fraction. The numerator and dominator are its two constituent parts, and they are present above and below the slash. The Division is represented by the slash in the fractions.
Most of the time, fractions are transformed into corresponding decimal values because writing mathematical operations in terms of decimal numbers makes them easier to do. Division, which appears to be the trickiest and most difficult mathematical operation, is typically used to convert fractions into decimal numbers.
Here, a fraction will be changed into a decimal using the Long Division method.
The process of converting 7/2 to its decimal equivalent is described in detail below.
Solution
We can solve a fraction by separating it into its parts based on how they perform their respective operations. As a result, the fraction’s denominator becomes the Divisor, and its numerator, the Dividend.
The fraction in this example contains dividend 7 and divisor 2 as shown below:
Dividend = 7
Divisor = 2
By dividing this fraction, we arrive at our outcome, also known as the Quotient.
Quotient = Dividend $\div$ Divisor = 7 $\div$ 2
The division procedure may not always be completed, leaving us with some leftover quantity. The term Remainder is used to refer to this leftover value.
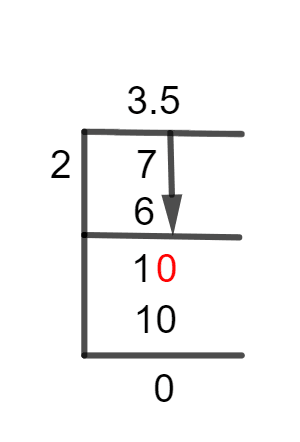
Figure 1
7/2 Long Division Method
The fraction that we are attempting to solve is:
7 $\div$ 2
One of the two basic rules of division is the use of Decimal points. According to this rule, the use of a decimal point is necessary whenever the dividend is less than the divisor and we get this decimal point if we multiply our dividend by 10. If a fraction has a greater dividend, though, we can continue without the decimal point.
According to the second rule, the division is performed by finding a divisor’s multiple closest to the dividend and then subtracting it from the dividend. If there is any value left over, it will serve as a dividend for the subsequent division. Moreover, once a decimal point has been added, we can multiply the remainder by 10, whenever it is less as compared to the divisor.
7 $\div$ 2 $\approx$ 3
Where:
2 x 3 = 6
The remaining value is obtained by subtracting 6 from 7.
7 – 6 =1
The remainder’s value 1 is now smaller than the divisor’s value 2, and it prevents us from moving forward without a decimal point. To generate a decimal point, we, therefore multiply 1 by 10.
10 $\div$ 2 $\approx$ 5
Where:
2 x 5 = 10
This time, we don’t have any value left.
10 – 10 =0
Therefore, we infer that the fraction 7/2, upon simplification, gives us a Quotient of 3.5 and a zero remainder.
Images/mathematical drawings are created with GeoGebra.
