What Is 7/4 as a Decimal + Solution With Free Steps

The fraction 7/4 as a decimal is equal to 1.75.
A Fraction is the proportion of two whole numbers. It has two elements: numerator and denominator, separated by a slash or line.
A fraction is said to be a Proper fraction if the denominator is greater than the numerator. On the other hand, it is referred to as an Improper Fraction if the numerator is greater.
As in our case, numerator 7 is greater than denominator 4, so it is an improper fraction.
Because decimal numbers are easier to understand, fractions are frequently converted to decimal numbers. A decimal number is a number with a decimal point that separates its fractional and whole number parts.
Division appears to be the most complex mathematical operation. However, it is not that difficult because there is a solution to this challenging problem. Long Division is the method for solving the fraction form problem.
We will convert the fraction 7/4 to a decimal number using the Long Division method.
Solution
Dividend and Divisor are terms used to describe the numbers that will be divided in the division process. In this scenario, we have to divide 7 by 4. Thus, 7 is the dividend, while 4 is the divisor. In mathematical form, it is stated as:
Dividend = 7
Divisor = 4
Once we are done with division, we obtain Quotient as a consequence. In some circumstances, we are unable to entirely divide two numbers and some remaining numbers. The remainder is the name given to this remaining value:
Quotient = Dividend $\div$ Divisor = 7 $\div$ 4
A thorough solution of 7/4 by adopting the method of Long Division is given below:
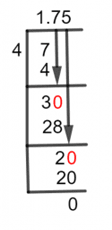
Figure 1
7/4 Long Division Method
7/4 can be written as follows:
7 $\div$ 4
As a result, in this division, the dividend 7 is divided by 4, and the divisor is 4. The stages are listed below. Since 7 is greater than 4, we can divide without using a decimal point:
7 $\div$ 4 $\approx$ 1
Where:
4 x 1 = 4
In order to find the value left remaining, we subtract 4 from 7:
7 – 4 =3
Therefore, since the remainder of 3 is less than the divisor, we proceed by adding a decimal point to the quotient. Then, to the right of the remainder, we add a zero to compensate for this.
As a result, we obtain 30 divided by 4:
30 $\div$ 4 $\approx$ 7
Where:
4 x 7 = 28
28 is subtracted from 30 to the left 2 as the remainder:
30 –28 = 2
We obtain 20 to divide from 4 after placing a 0 to the right of 2:
20 $\div$ 4 $\approx$ 5
Where:
4 x 5 = 20
Remainder is:
20 –20 =0.
As 1.75 is a decimal value of 7/4, the fraction is fully solved as indicated by the zero remainder.

Images/mathematical drawings are created with GeoGebra.
