What Is 7/5 as a Decimal + Solution With Free Steps

The fraction 7/5 as a decimal is equal to 1.4.The mathematical procedure of division between two numbers is expressed using Fractions. When these integers are divided by one another, an incomplete division yields a decimal value as the outcome.Now, we use a technique known as a Long division to solve the division operation when a number doesn’t divide equally across the others. First, let’s examine the fraction 7/5 long division solution.

Solution

The first step in solving a fraction problem is determining if it is a proper or improper fraction. A proper fraction contains a greater denominator than an improper fraction, which has a greater numerator.A fractional problem is solved by converting it into a division problem. To do this, classify the component pieces or elements according to their performance. The term Denominator refers to the Divisor, whereas dividend refers to the Numerator or the number that will be divided:

Dividend = 7

Divisor = 5

The Quotient, described as the result of a division, will be introduced in this section:

Quotient = Dividend $\div$ Divisor = 7 $\div$ 5

As we can see, this fraction has now been divided, and to determine the quotient, we must use the long division method to solve this: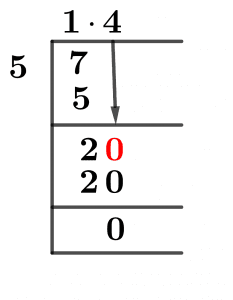

Figure 1

7/5 Long Division Method

Now we begin stating our problem by the division criterion:

7 $\div$ 5

This division expression can provide a lot of information about the Quotient.The Dividend and the Divisor directly impact the Quotient in their ways. And this is where the quotient is greater than one if the dividend is greater than the divisor and vice versa if the dividend is smaller than the divisor.Since 5 is greater than 2, our quotient would be greater than 1 in this case.And now we reach the subject of Remainder. The Remainder is much more than the value that remains after an inconclusive division, as we know. In our long division method, the remaining amount perpetually becomes the next Dividend.Now that we can see that our dividend is more than the divisor, we can quickly solve the problem:

7 $\div$ 5 $\approx$ 1

Where:

5 x 1 = 5 

The remainder is, therefore, equal to:

7 – 5 = 2

Because the remainder becomes the new dividend, we now have a recent Dividend of 2. We put a decimal point in and receive a zero for the dividend because we can see that it is smaller than the divisor.As a result, our new dividend is 20:

20 $\div$ 5 = 4

Where:

5 x 4 = 20

So the remainder is, therefore, equal to:   

20 – 20 = 0

As a result, a Remainder of zero is generated. This proves that the Conclusive division existed and we have a quotient of 1.4.Images/mathematical drawings are created with GeoGebra.