What Is 9/4 as a Decimal + Solution With Free Steps

The fraction 9/11 as a decimal is equal to 0.8181.A fraction can also be expressed in the form of a decimal number. Fraction is a fundamental math concept that can be found everywhere, from everyday life to high school homework. A fraction represents an operation where one number has been cut down and reduced in size by another number or numbers called “dividers.”Decimal numbers are often used in math and science because they allow you to represent whole numbers and fractional parts. For example, 3/10 means three out of ten or 30%.There are different types of decimal numbers, such as recurring or repeating decimal numbers and non-recurring or non-repeating decimal numbers. A decimal number in which digits repeat recurrently is called a recurring decimal. In contrast, the decimal numbers in which the digits do not repeat themselves regularly are called non-recurring decimal numbers.The decimal equivalent of the fraction 9/11 is 0.81818181, which shows that it is a recurring decimal number as 81 is repeating itself infinitely. Let’s find out how to determine the decimal equivalent of 9/11.

Solution

In the given fraction, the dividend and divisor are the following:

Dividend = 9 

Divisor = 11

This shows that the dividend is smaller than the divisor. To solve the given fraction, it is required to add a decimal point and make the dividend bigger than the divisor by adding a zero to it. The fractional division for 9/11 is shown below in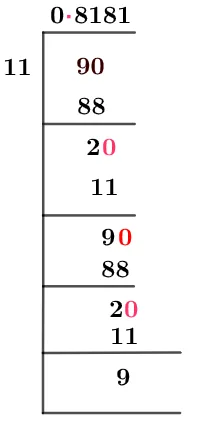 figure 1:

9/11 Long Division Method

The long division method can be easily explained as below:

Dividend $\div$ Divisor = Quotient

9 $\div$ 11 = 0.8181

Now let us have a detailed analysis of this division. Firstly, when starting with the division process, it has been noticed that nine is smaller than 11 and hence cannot be directly divided. So, to divide it into equal pieces, a decimal point is added to the quotient and a zero to the dividend.The above process converts 9 to 90, which is bigger than 11. Now continuing with the division gives:

90 $\div$ 11 $\approx$ 8

As it can be seen that:

11 x 8 = 88

Therefore the remainder is 2 in this case. Again adding a zero gives 20 as a dividend. Now dividing 20 by 11 gives:

20 $\div$ 11 $\approx$ 1

Where:

11 x 1 = 11

So, the remainder left is 9. Since the remainder is not equivalent to zero, we can continue with the division process. For making 9 bigger than 11, add a zero to the dividend, and it will become 90.

90 $\div$ 11 $\approx$ 8

Where:

11 x 8 = 88

The remainder is 2. This shows that a similar pattern is obtained as the division proceeds. A decimal number in which the digits repeat themselves periodically or in a specific way is called recurring decimals. Therefore, the decimal equivalent of the fraction 9/11 is a recurring decimal.Images/mathematical drawings are created with GeoGebra.