What Is 1 1/4 as a Decimal + Solution With Free Steps
The fraction 1 1/4 as a decimal is equal to 1.25.
A Mixed Fraction is created, when a whole number and a proper fraction are represented together. For instance, a whole number 1 and a proper fraction 1/4, when represented together give a mixed fraction of 11/4.
Typically, a mixed fraction is used to express a number that falls between two whole integers. Since decimal numbers are easy to use in mathematical calculations than fractions, these fractions are frequently converted into decimal numbers having a fractional part and a whole number part separated by a decimal point.
There are numerous ways to do this. One is the Long Division approach, which is described in more detail below, for changing 1 1/4 to its decimal number.
Solution
The first step in solving a mixed fraction is its conversion into an Improper Fraction. To do this we add the product of 1, the whole number, and 4, the denominator to 1, the numerator. The resultant value, which we get is the numerator of improper fraction while its denominator will be the same as that of mixed fraction. Thus, we get an improper fraction, 5/4 to solve.
Now, we will solve 5/4. This means that 5 is the Dividend and 4 is the Divisor.
Dividend = 5
Divisor = 4
This division gives us a result which we call Quotient.
Quotient = Dividend $\div$ Divisor = 5 $\div$ 4
If in a division process, the dividend is not a multiple of divisor, we are left with some value, which is called the Remainder.
Below is the detailed description of the conversion of 5/4 to decimal by the method of Long Division.
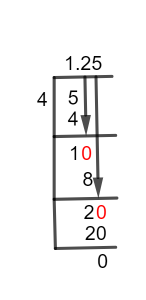
Figure 1
1 1/4 Long Division Method
Hence, we are going to solve 5/4 by the Long Division method.
5 $\div$ 4
In the division process, the closest multiple of the divisor to the dividend is found and then subtracted from the dividend. So, here to divide 5 by 4, we will subtract the closest multiple of 4 from 5 i.e., 4
5 $\div$ 4 $\approx$ 1
Where:
4 x 1 = 4
The remainder is determined as:
5 – 4 = 1
1 is the remainder, which is less than 4, the divisor. So, now we will introduce a Decimal Point in the quotient and multiply the remainder 1 by 10. By doing so, we get 10 to be divided by 4.
10 $\div$ 4 $\approx$ 2
Where:
4 x 2 = 8
The remaining value is computed as:
10 – 8 = 2
This 2 becomes 20 when multiplied by 10. So, now we have 20 to divide from 4.
20 $\div$ 4 $\approx$ 5
Where:
4 x 5 = 20
Remaining value is 20 – 20 =0
This time, we get a zero Remainder, which indicates that 1.25 is the equivalent Decimal Value of fraction 1 1/4.
Images/mathematical drawings are created with GeoGebra.
