What Is 1/16 as a Decimal + Solution With Free Steps
The fraction 1/16 as a decimal is equal to 0.0625.
A Fraction is a mathematical expression that shows how many parts we can divide a number. In a fraction, a line divides the numerator and denominator, which are its components. The number present above the line is the Numerator, and the number below the line is the Denominator.
The given example shows the conversion of a fraction 1/16 into its decimal by the Long Division method.
Solution
The best way to solve a fraction is by converting it to division. Components of the division include Dividend and Divisor, which represent the number that is divided and the number that is dividing, respectively.
When we transform 1/16 into a division, we get a dividend equal to 1 and a divisor equal to 16.
Dividend = 1
Divisor = 16
After solving this fraction, we get a result in the form of a Quotient. But sometimes, we are unable to solve a fraction completely and get some left-over number, which is known as a Remainder.
Quotient = Dividend $\div$ Divisor = 1 $\div$ 16
Here, the solution of fraction 1/16 by using the method of Long Division is presented.
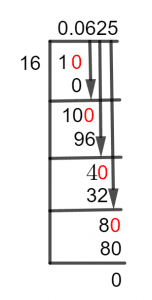
Figure 1
1/16 Long Division Method
We have the fraction as:
1 $\div$ 16
To simplify any fractional expression, we first determine if it is a Proper or an Improper Fraction. In the case of a proper fraction, the equivalent decimal value is less than 1, and a Decimal point is required.
As in the given example, as 1 is less than 16, so we must insert a Decimal Point in the quotient. This is done by multiplying the dividend 1 by 10. Hence, we get 10 to divide by 16.
In the division process, first, the multiple of the divisor that is closest to the dividend is determined and then it is subtracted from the dividend. Thus, we multiply 16 by zero and then subtract it from 10.
10 $\div$ 6 $\approx$ 0
Where:
16 x 0 = 0
A remainder of 16 is produced.
10– 0 = 10
Now, we again multiply the remainder by 10, but without adding any decimal point, because it is already present in the quotient.
Therefore, now we have 100 to divide by 16.
100 $\div$ 6 $\approx$ 6
Where:
16 x 6 = 96
The remaining value is calculated as:
100– 96 = 4
Remainder 4 becomes 40 by multiplying it with 10.
40 $\div$ 16 $\approx$ 2
Where:
16 x 2 = 32
40– 32 = 8 is the remainder and we make it 80 by the multiplication with 10. We proceed with our calculations as follows:
80 $\div$ 16 $\approx$ 5
Where:
16 x 5 = 80
As 80 is a multiple of 16, so we get no remaining value this time.
80– 80 = 0
This shows that the fraction is completely simplified and 0.0625 is calculated as the Quotient.
Images/mathematical drawings are created with GeoGebra.
