What Is 1/20 as a Decimal + Solution With Free Steps
The fraction 1/20 as a decimal is equal to 0.05.
The number of equally sized components that make up a whole is expressed as a Fraction. Simple fractions are straightforward to recognize since they have two integers that are separated by a line or slash.
The number preceding the slash is known as the Numerator. It reveals how many parts we have. On the other hand, the integer below the slash is known as the Denominator. It tells us about the total number of parts.
The need to convert fractions into decimals arises frequently since doing so makes the fraction simpler to comprehend and understand.
Additionally, it is simple to tell which decimal number is larger and which is smaller by comparing two decimal values. However, concluding such results by the comparison of two fractions is difficult.
In this article, we will solve 1/20 and find its decimal value.
Solution
Before solving a fraction, we first determine whether it is a Proper or Improper Fraction, and then we convert it into division. Proper fraction means that the numerator is lesser as compared to the denominator and its decimal value is always less than 1. Whereas, in an improper fraction, the denominator is lesser, and its decimal value is always greater than 1.
In this case, 1/20 is a proper fraction. To divide this fraction, we transform it into division by distinguishing its elements according to the functions they perform. Hence, we get numerator 1 as a Dividend and denominator 20 as a Divisor.
Dividend = 1
Divisor = 20
The other two division-specific terms are Quotient and Remainder. The quotient is the result we finally obtain after completing our division. But if two numbers are not fully divided, we get some left-over quantity. This is called Remainder.
Quotient = Dividend $\div$ Divisor = 1 $\div$ 20
To solve this fraction, we use the Long Division method, as shown below.
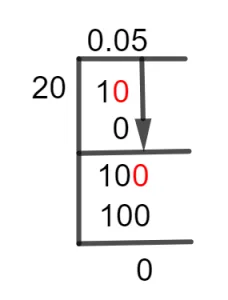
Figure 1
1/20 Long Division Method
We are given a proper fraction of 1/20 to solve.
1 $\div$ 20
Since 1/20 is a proper fraction i.e., the dividend is smaller than the divisor, so to perform calculation, we need a Decimal Point. To get this decimal point, we will place a zero to the right of the dividend and make it 10 and it can be divided by 20, as shown below.
10 $\div$ 20 $\approx$ 0
Where:
20 x 0 = 0
The remainder is calculated to be 10 as shown below:
10 – 0 = 10
To continue, we again place a zero to the right of the remainder, which then becomes 100.
100 $\div$ 20 $\approx$ 5
Where:
20 x 5= 100
The remaining value is zero.
100 – 100 = 0
A zero Remainder shows that the fraction is solved completely and has a decimal value of 0.05.
Images/mathematical drawings are created with GeoGebra.
