What Is 2/10 as a Decimal + Solution With Free Steps
The fraction 2/10 as a decimal is equal to 0.2.
A Fraction is an expression that can be used to express the ratio of two integers in the form of p/q. The Numerator and Denominator, which are separated by a line, are the two elements of a fraction. These are present above and below the line, respectively.
Fractions are usually converted into equivalent Decimal Numbers because decimal numbers are easier to understand. For example, if we want to find a larger of two fractions with different numerators and denominators, it would be difficult. But we can do it easily by looking at their corresponding decimal values.
Long Division is the method that is mostly used to solve a fraction. In this method, large numbers are divided by splitting them into smaller groups.
Here, we will find the decimal value of 2/10 using the Long Division method.
Solution
The decimal value of a fraction is obtained by dividing its fractional components numerator and denominator. So we take a numerator as a Dividend, defined as the number we have to divide, and a denominator as a Divisor, a number that will divide the other.
The fraction of 2/10, which we have to solve, is represented as:
Dividend = 2
Divisor = 10
If the division is performed completely, we get our final result, which we call the Quotient.
Quotient = Dividend $\div$ Divisor = 2 $\div$ 10
In some cases, we cannot solve a fraction completely and we get some remaining quantity. This remaining quantity is called Remainder.
We will solve the fraction 2/10 here to find its quotient and remainder.
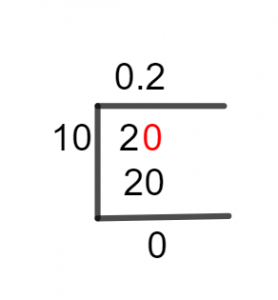
Figure 1
2/10 Long Division Method
The complete procedure to solve a fraction of 2/10 utilizing the method of Long Division is given below.
We have:
2 $\div$ 10
Finding the greater number between the numerator and denominator is the first step in solving a fraction.
The solution requires a Decimal Point if the numerator is greater than the denominator. which we get by adding a zero to the dividend’s right. However, if the denominator is greater, we don’t need a decimal point.
In the fraction of 2/10, the dividend 2 is smaller as compared to divisor 10. So, this is a Proper Fraction and we require a decimal point for the quotient. We get this by adding a zero to the right of 2 and making it 20. This 20 can now be easily divided by 10.
20 $\div$ 10 $\approx$ 2
Where:
10 x 2 = 20
Since 20 is a multiple of 10, so we don’t get any remaining value.
20 – 20 = 0
Thus, our fraction is solved completely and we get our final result i.e., Quotient equal to 0.2 without any remainder. This shows that we can divide 2 into 10 equal parts and the size or magnitude of each part will be equal to 0.2.
Images/mathematical drawings are created with GeoGebra.
