What Is 2/9 as a Decimal + Solution With Free Steps
The fraction 2/9 as a decimal is equal to 0.222.
We use Fractions to express the relationship between two numbers where one is Divided across another. And when we use said Fractions for such an expression, they produce Decimal Numbers as their result. This is because these dividing numbers are not in the same Multiplicative family and thus produce numbers that lie between Integers.
A Decimal Number, therefore, has two parts, one is the Whole Number part which represents the integer from which it is bigger. The other one corresponds to the amount it is bigger than the integer in Decimal Points, and thus a decimal number is formed.
Now, the method used for Solving said fraction into a decimal number is called the Long Division Method. Thus, let’s go through the solution of this fraction 2/9.
Solution
So we start by separating the Fraction into the division components, this is done by converting the numerator into the Dividend and the denominator into the Divisor. This can be seen done here:
Dividend = 2
Divisor = 9
Now, to understand the concept of Division better, we take the dividend of 2 and break it down into 9 pieces. Each of these pieces will now be equal to the division, so any one of these is represented by the Fraction here. Thus, we have our Quotient equal to this:
Quotient = Dividend $\div$ Divisor = 2 $\div$ 9
Hence, without further ado we will go into the solution of our fraction using Long Division Method:
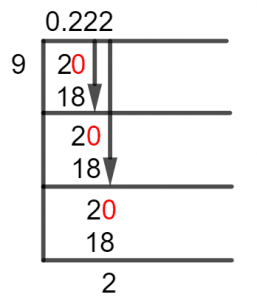
Figure 1
2/9 Long Division Method
We begin by Analyzing the dividend against the divisor, as our dividend is Smaller than the divisor, we take 2 and multiply it by 10. This is done by placing a Decimal Point in the quotient, and this decimal then has a Whole Number equal to 0. So, let’s solve for 20/9 as follows:
20 $\div$ 9 $\approx$ 2
Where:
9 x 2 = 18
Which generated a Remainder equal to 20 – 18 = 2, this means that our divisor 9 was not a Factor of the dividend 20. As we know that the Remainder after one iteration of division becomes the new dividend. We make the new dividend i.e., 2 into a bigger Dividend than the divisor, which is done by multiplying it by 10.
20 $\div$ 9 $\approx$ 2
Where:
9 x 2 = 18
Again, a Remainder of 20 – 18 = 2 is generated, and we can see that this is the same remainder that was generated in the last division. So the next one would be the same as well, and we won’t be solving for that.
Hence, we will finalize our division based on data we have found, and that is a Repeating Number 2 in the Quotient. Therefore, we have on our hands a Repeating Decimal Number, and this number is expressed as a Quotient of 0.222.
Images/mathematical drawings are created with GeoGebra.
