What Is 3 1/2 as a Decimal + Solution With Free Steps
The fraction 3 1/2 as a decimal is equal to 3.5.
When two whole numbers are written in the form of a ratio as p/q, they are referred to as a Fraction. Here p represents the Numerator and q represents the Denominator of a fraction. The separation indicates this expression to be a fraction. Any numbers written in the form of p/q are called fractions.
A Mixed Fraction is a certain type of fraction which is formed by the combination of a proper fraction and a whole number. It is obtained from an improper fraction by writing its quotient as the whole number and remainder as the numerator.
Usually, Decimal Numbers are preferred to be used in mathematical computations because they are easy to comprehend. The most common method used for converting fractions into decimals is the Long Division method.
In this example, we have a fraction of 3 1/2, which will be converted into a decimal using the Long Division.
Solution
A mixed fraction must first be transformed into an improper fraction before being converted into a decimal number. For this conversion, the denominator of the mixed fraction must be multiplied by its whole number and the result thus obtained is added to the numerator.
The outcome we get is the numerator of the improper fraction and there will be no change in the denominator.
In the fraction given to solve, 2 is multiplied by 3, and the product is added to 1, which gives 7 as the numerator of the improper fraction. While its denominator is 2. Thus, our desired fraction is 7/2.
Thus, to get the decimal value of 3 1/2, 7 is divided by 2. Thus, we have:
Dividend = 7
Divisor = 2
Our ultimate result, known as the quotient, is obtained by dividing this fraction.
Quotient = Dividend \div Divisor = 7 \div 2
Sometimes, we are left with some remaining quantity because the division process is not completed. This left-over quantity is given the name Remainder.
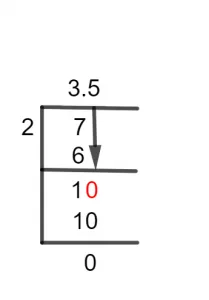
Figure 1
3 1/2 Long Division Method
The fraction to be solved is:
7 $\div$ 2
Whenever there is a dividend smaller than the divisor, there is a requirement of a Decimal Point. On the other hand, we can move on without the decimal point if a fraction has a larger dividend.
7 $\div$ 2 $\approx$ 3
Where:
2 x 3 = 6
When we subtract 6 from 7, we get the remaining value as:
7 – 6 =1
We are now unable to continue without a decimal point because the value of the remainder 1 is less than 2, the divisor. Thus, we multiply 1 by 10 to get a decimal point.
10 $\div$ 2 $\approx$ 5
Where:
2 x 5 = 10
We don’t have any remainder now.
Therefore 10 – 10 =0.
Therefore, we conclude that the fraction of 3 1/2 can be solved completely, and the Quotient’s value is 3.5 without any remainder.
Images/mathematical drawings are created with GeoGebra.
