What Is 3 1/5 as a Decimal + Solution With Free Steps
The fraction 3 1/5 as a decimal is equal to 3.2.
Fraction is a very important concept of mathematics. It helps us to determine how many equal portions may combine to make a whole object. Its important types include proper fractions, improper fractions, and mixed fractions.
When a fraction’s denominator is greater than its numerator, it is termed a Proper Fraction, but when a fraction has a greater numerator, it is referred to as an Improper Fraction. In many cases, a fraction is formed by combining a whole number and a proper fraction, such a fraction is known as Mixed Fraction.
A fraction is simplified to get its decimal number, which has a decimal point separating a fractional part and a whole number part. For example, 3.2 where 2 is the fractional part and 3 is the whole number part.
In this question, we will get a decimal value of 3 1/5 by the Long Division method.
Solution
We solve a mixed fraction by first converting it into an Improper Fraction. For this, we do the multiplication of denominator 5 with 3 and then add this product 15 to the numerator 1.
As a result, we get 16, which is the numerator of the desired improper fraction. However, its denominator is also 5. Hence, we get a fraction of 16/5 to solve.
We can see that in 16/5, 16 is Dividend, and 5 is Divisor.
Dividend = 16
Divisor = 5
The decimal number obtained as a result of the division of the numerator by the denominator of the fraction is known as Quotient.
Quotient = Dividend $\div$ Divisor = 16 $\div$ 5
There are some situations when division cannot be completed, and we are left with a quantity known as the Remainder.
The conversion of 3 1/5 into its decimal value is shown below.
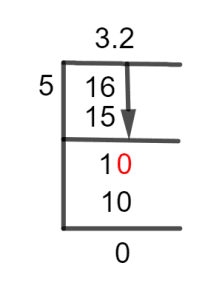
Figure 1
3 1/5 Long Division Method
The fraction we are supposed to solve is:
16 $\div$ 5
To divide a fraction, a Decimal Point is to be added whenever the dividend is less than the divider. But if we have a divisor or divider less than the dividend, we don’t need any decimal point. In the fraction of 16/5, 16 is a bigger number so we will divide it directly without any decimal point.
16 $\div$ 5 $\approx$ 3
Where:
5 x 3 = 15
The left-over value or remainder is found to be:
16 – 15 =1
This remainder 1 is less than the divider and it indicates that now we need a decimal point for further calculations. We get this decimal point if we multiply our remainder by 10.
After this multiplication, we get 10 to divide by 5.
10 $\div$ 5 $\approx$ 2
Where:
5 x 2 = 10
The remainder 10 – 10 = 0 shows that 3 1/5 is a Terminating and Non-recurring fraction and has a Quotient equal to 3.2.
Images/mathematical drawings are created with GeoGebra.
