What Is 4/10 as a Decimal + Solution With Free Steps
The fraction 4/10 as a decimal is equal to 0.4.
A Fraction is a very special way of expressing a mathematical operation, it is equivalent to the Dot used in expressing multiplication. A Fraction is therefore generally used to express a division between two numbers, but it’s the kind of Division that doesn’t solve into an integer.
As we know, this kind of division is expressed as a fraction and doesn’t produce an Integer, we come to find that this division produces a Decimal Value. A Decimal number is best known as one which has two parts, a Whole Number part, and a Decimal part. Its value lies between two Integers.
So, we will solve the fraction given to us as 4/10 using the method for solving this kind of division, the Long Division Method.
Solution
We start off solving a Fraction into a division by first converting a said fraction into a division. That is done by Transforming the components of a fraction into a division. As we know, the Dividend is equivalent to the numerator, and the Divisor is equivalent to the denominator. Hence, we express our Fraction now as:
Dividend = 4
Divisor = 10
Now, if we analyze the Division that we have, we conclude that 4 our Dividend is being broken down into 10 pieces. And one of those pieces is then expressed as the Quotient i.e., the Solution of this division. This is also what the Fraction was expressing, so we have:
Quotient = Dividend $\div$ Divisor = 4 $\div$ 10
Finally, we will go through the Long Division Solution to this problem:
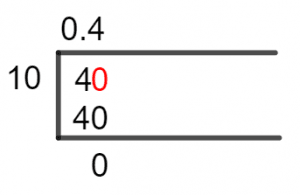
Figure 1
4/10 Long Division Method
Solving a division using Long Division, we have to keep in mind two rules on which it operates. The First Rule is that when the dividend is Smaller than the divisor, we introduce the decimal point in the Quotient and multiply the dividend by 10. The Second Rule states that we find the Multiple of the divisor closest to the dividend and then Subtract the multiple from it.
Now the solution of the Subtraction then becomes the dividend for the next iteration of division, and it is called the Remainder. Also, once the Decimal Point is brought in, then we can always multiply the dividend by 10 if it’s Smaller than the divisor.
Finally, we look at our dividend of 4 Smaller than 10, so we have to make it bigger than the Divisor. We already know that under such circumstances we use the first rule of the Long Division and multiply the dividend by 10.
But this also adds a decimal point to the Quotient, and this means we have a quotient with 0 Whole Number and no Decimal Number. The Dividend, hence, becomes 40 and the solution is:
40 $\div$ 10 = 4
Where:
10 x 4 = 40
Therefore, no Remainder is generated, and a Quotient with a value of 0.4 is found.
Images/mathematical drawings are created with GeoGebra.
